Advertisements
Advertisements
प्रश्न
If P is any point in the interior of a parallelogram ABCD, then prove that area of the
triangle APB is less than half the area of parallelogram.
उत्तर
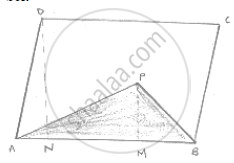
Draw DN ⊥ AB and PM ⊥ AB.
Now,
`Area (ΙΙ^(gm) ABCD) = AB xx DN , ar (ΔAPB ) = 1/2 (AB xx PM)`
Now , PM < DN
⇒ `AB xx PM < AB xx DN`
⇒ ` 1/2 (AB xx PM) < 1/2 (AB xx DN)`
⇒ `Area ( ΔAPB ) <1/2 ar ( Parragram ABCD)`
APPEARS IN
संबंधित प्रश्न
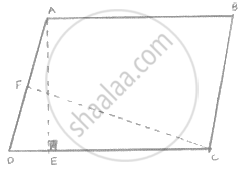
In fig below, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8
cm and CF = 10 cm, find AD.
ABCD is a parallelogram. E is a point on BA such that BE = 2 EA and F is a point on DC
such that DF = 2 FC. Prove that AE CF is a parallelogram whose area is one third of the
area of parallelogram ABCD.
If ABC and BDE are two equilateral triangles such that D is the mid-point of BC, then find ar (ΔABC) : ar (ΔBDE).
In the given figure, find the area of ΔGEF.
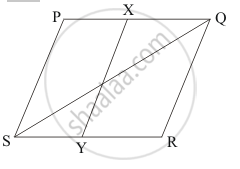
In the given figure, PQRS is a parallelogram. If X and Y are mid-points of PQ and SRrespectively and diagonal Q is joined. The ratio ar (||gm XQRY) : ar (ΔQSR) =
The perimeter of a triangle ABC is 37 cm and the ratio between the lengths of its altitudes be 6: 5: 4. Find the lengths of its sides.
Let the sides be x cm, y cm, and (37 - x - y) cm. Also, let the lengths of altitudes be 6a cm, 5a cm, and 4a cm.
The side of a square field is 16 m. What will be increase in its area, if each of its sides is increased by 4 m?
Who had the bigger piece? How much bigger?
Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- The cost of one book is Rs 47. Sonu buys 23 books.
a) How much money does she have? b) How much money does she pay for the books? c) What is the cost of 47 books?
Find the area of the following figure by counting squares:

