Advertisements
Advertisements
प्रश्न
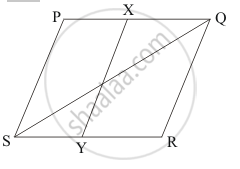
In the given figure, PQRS is a parallelogram. If X and Y are mid-points of PQ and SRrespectively and diagonal Q is joined. The ratio ar (||gm XQRY) : ar (ΔQSR) =
पर्याय
1 : 4
2 : 1
1 : 2
1 : 1
उत्तर
Given: (1) PQRS is a parallelogram.
(2) X is the midpoint of PQ.
(3) Y is the midpoint of SR.
(4) SQ is the diagonal.
To find: Ratio of area of ||gm XQRY : area of ΔQRS.
Calculation: We know that the triangle and parallelogram on the same base and between the same parallels are equal in area.
∴ Ar (||gm PQRS) = Ar (ΔQRS)
`Ar ( "||"^(gm) XQRY ) = 1/2 Ar ("||"^(gm) PQRS)`
(since X is the mid point of PQ and Y is the midpoint of SR)
`Ar ("||"^(gm) XQRY) = Ar (ΔQRS)`
`Ar ("||"^(gm) XQRY ) : Ar (ΔQRS) = 1:1`
APPEARS IN
संबंधित प्रश्न
In the below Fig, ABC and ABD are two triangles on the base AB. If line segment CD is
bisected by AB at O, show that ar (Δ ABC) = ar (Δ ABD)

If P is any point in the interior of a parallelogram ABCD, then prove that area of the
triangle APB is less than half the area of parallelogram.
In the given figure, find the area of ΔGEF.
ABCD is a parallelogram. P is any point on CD. If ar (ΔDPA) = 15 cm2 and ar (ΔAPC) = 20 cm2, then ar (ΔAPB) =
In a ΔABC if D and E are mid-points of BC and AD respectively such that ar (ΔAEC) = 4cm2, then ar (ΔBEC) =
ABCD is a trapezium with parallel sides AB =a and DC = b. If E and F are mid-points of non-parallel sides AD and BC respectively, then the ratio of areas of quadrilaterals ABFEand EFCD is
The length and breadth of a rectangular piece of land are in the ratio 5 : 3. If the total cost of fencing it at the rate of ₹24 per meter is ₹9600, find its :
(i) length and breadth
(ii) area
(iii) cost of levelling at the rate of ₹60 per m2.
Which has the bigger area - one of your footprints or the page of this book?
Which has the smaller area - two five-rupee notes together or a hundred rupee notes?
A magazine charges Rs 300 per 10 sq cm area for advertising. A company decided to order a half page advertisment. If each page of the magazine is 15 cm × 24 cm, what amount will the company has to pay for it?
