Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram. P is any point on CD. If ar (ΔDPA) = 15 cm2 and ar (ΔAPC) = 20 cm2, then ar (ΔAPB) =
पर्याय
15 cm2
20 cm2
35 cm2
30 cm2
उत्तर
Given: (1) ABCD is a parallelogram
(2) P is any point on CD
(3) Area of ΔDPA = 15 cm2
(4) Area of ΔAPC = 20 cm2
To find: Area of ΔAPB
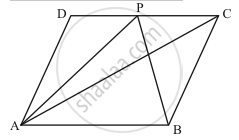
Calculation: We know that , “If a parallelogram and a a triangle are on the base between the same parallels, the area of triangle is equal to half the area of the parallelogram.”
Here , ΔAPB and ΔACB are on the same base and between the same parallels.
(since AC is the diagonal of parallelogram ABCD, diagonal of a parallelogram divides the parallelogram in two triangles of equal area)
ar (ΔACB ) = ar (ΔAPB)
ar (ΔACB) = ar (ΔADC)
ar (ΔACB) = Area of ΔADP + Area of ΔAPC
= 20 +15
= 35 cm2
Area of ΔACB = 35 cm2
APPEARS IN
संबंधित प्रश्न
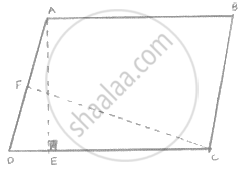
In fig below, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8
cm and CF = 10 cm, find AD.
If ABCD is a parallelogram, then prove that
𝑎𝑟 (Δ𝐴𝐵𝐷) = 𝑎𝑟 (Δ𝐵𝐶𝐷) = 𝑎𝑟 (Δ𝐴𝐵𝐶) = 𝑎𝑟 (Δ𝐴𝐶𝐷) = `1/2` 𝑎𝑟 (||𝑔𝑚 𝐴𝐵𝐶𝐷) .
In the given figure, find the area of ΔGEF.
In a ΔABC, D, E, F are the mid-points of sides BC, CA and AB respectively. If ar (ΔABC) = 16cm2, then ar (trapezium FBCE) =
Medians of ΔABC intersect at G. If ar (ΔABC) = 27 cm2, then ar (ΔBGC) =
Each side of a square is 7 m. If its each side be increased by 3 m, what will be the increase in its area.
The table given below contains some measures of the rectangle. Find the unknown values.
| Length | Breadth | Perimeter | Area |
| 13 cm | ? | 54 cm | ? |
Look at a 10 rupee note. Is its area more than hundred square cm?
Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- 352 children from a school went on a camping trip. Each tent had a group of 4 children.
a) How many children did each tent have? b) How many tents do they need? c) How many children in all are in the school?
Find the area of the following figure by counting squares:

