Advertisements
Advertisements
प्रश्न
Medians of ΔABC intersect at G. If ar (ΔABC) = 27 cm2, then ar (ΔBGC) =
पर्याय
6 cm2
9 cm2
12 cm2
18 cm2
उत्तर
Given: (1) Median of ΔABC meet at G.
(2) Area of ΔABC = 27 cm2
To find: Area of ΔBCG.
We know that the medians of the triangle divides each other in the ratio of 2:1
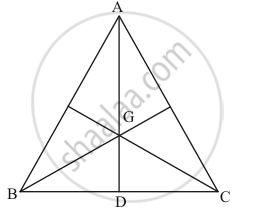
Hence,
ar (ΔBED) = `1/2 xx BC xx GD`
ar (ΔBED) =`1/2 xx BC xx 1/3 (AD)`
ar (ΔBED) =`1/3(1/2xx AD xx BC)`
ar (ΔBED) =`1/3 (Δ ABC)`
ar (ΔBED) = = `1/3(27)`
ar (ΔBED) == 9 cm2
APPEARS IN
संबंधित प्रश्न
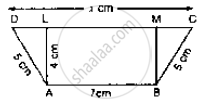
In the below fig. ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm,
and distance between AB and DC is 4cm. Find the value of x and area of trapezium ABCD.
Two parallelograms are on the same base and between the same parallels. The ratio of their areas is
In the given figure, ABCD is a parallelogram. If AB = 12 cm, AE = 7.5 cm, CF = 15 cm, then AD =

ABCD is a rectangle with O as any point in its interior. If ar (ΔAOD) = 3 cm2 and ar (ΔABOC) = 6 cm2, then area of rectangle ABCD is
The medians of a triangle ABC intersect each other at point G. If one of its medians is AD,
prove that:
(i) Area ( ΔABD ) = 3 x Area ( ΔBGD )
(ii) Area ( ΔACD ) = 3 x Area ( ΔCGD )
(iii) Area ( ΔBGC ) = `1/3` x Area ( ΔABC ).
Is the area of your belt the same as the area of the postcard? Why or why not?
Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- 352 children from a school went on a camping trip. Each tent had a group of 4 children.
a) How many children did each tent have? b) How many tents do they need? c) How many children in all are in the school?
Area of a rectangle with length 5 cm and breadth 3 cm is ______.
Is the area of both your footprints the same?
Find the area of the following figure by counting squares:

