Question

ABCD is a rectangle with O as any point in its interior. If ar (ΔAOD) = 3 cm² and ar (ΔABOC) = 6 cm², then area of rectangle ABCD is

पर्याय

• 9 cm²

• 12 cm²

• 15 cm²

• 18 cm²

Answer 1

Given: A rectangle ABCD , O is a point in the interior of the rectangles such that

(1) ar (ΔAOB) = 3 cm²

(2) ar (ΔBOC) = 6 cm²

To find: ar (rect.ABCD)

Construction: Draw a line LM passing through O and parallel to AD and BC.

Calculation: We know that ,” If a triangle and a parallelogram are on the same base and between the same parallels the area of the triangle is equal to half the area of the parallelogram”

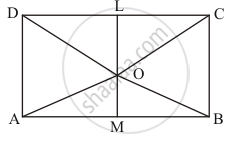
Here we can see that ΔAOD and rectangle AMLD are on the same base AD and between the same parallels AD and LM.

Hence ,

ar (Δ AOD) = `1/2` (rect . ALMD) 

ar (rect ALMD )= 2 ar (ΔAOD) 

ar (rect . ALMD) = 2(3)

ar (rect . ALMD ) = 6 cm²   .....................(1)

Similarly, we can see that ΔBOC and rectangle BCLM are on the same base BC and between the same parallels BC and LM

Hence,

ar(ΔBOC ) = `1/2` ar (rect . BCLM)

ar (rect BCLM) = 2ar (ΔBOC) 

ar (rect .aBCLM) = 12 cm²

ar (rect . bclm) = 12 cm²               .................(2)

We known that

ar (rect . ABCD) = ar (rect . ALMD) + ar (rect . BCLM) 

ar (rect . ABCD) =  6 +12

ar (rect . ABCD) = 18 cm²