Question

ABCD is a trapezium with parallel sides AB =a and DC = b. If E and F are mid-points of non-parallel sides AD and BC respectively, then the ratio of areas of quadrilaterals ABFEand EFCD is

पर्याय

• a : b

• (a + 3b): (3a + b)

• (3a + b) : (a + 3b)

•  (2a + b) : (3a + b)

Answer 1

Given: (1) ABCD is a trapezium, with parallel sides AB and DC

(2) AB = a cm

(3) DC = b cm

(4) E is the midpoint of non parallel sides AD.

(5) G is the midpoint of non parallel sides BC.

To find: Ratio of the area of the Quadrilaterals ABFE and EFCD.

Calculation: We know that, ‘Area of a trapezium is half the product of its height and the sum of the parallel sides.’

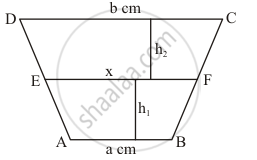
Since, E and F are mid points of AD and BC respectively, so h₁ = h₂

Area of trapezium ABFE

Area of trapezium ABFE`=1/2 (a + x) h_1 = 1/2 (a + x)h`

Area of trapezium EFCD = `1/2 (b+x)h_2 = 1/2 (b+ x) h`

Area of trapezium ABCD `= 1/2 (a+ b) (h_1 + h_2 ) = (a+b) h`

Now, Area (trap ABCD) = area (trap EFCD) + Area (ABFE)

Therefore,

(a + b) h = `1/2 ( a + x) h + 1/2 (b+x) h`

`⇒ A +b = (a+b)/2 +x`

`⇒x = (a+b)/2`

Thus,

`(Area  (ABFE))/(Area (EFCD)) = (a+x)/(b +x) = (a +(a+b)/2)/(b + (a+b)/2)`

`⇒ (Area (ABFE))/(Area (EFCD)) = (3a +b)/(a + 3b)`