Advertisements
Advertisements
Question
ABCD is a trapezium with parallel sides AB =a and DC = b. If E and F are mid-points of non-parallel sides AD and BC respectively, then the ratio of areas of quadrilaterals ABFEand EFCD is
Options
a : b
(a + 3b): (3a + b)
(3a + b) : (a + 3b)
(2a + b) : (3a + b)
Advertisements
Solution
Given: (1) ABCD is a trapezium, with parallel sides AB and DC
(2) AB = a cm
(3) DC = b cm
(4) E is the midpoint of non parallel sides AD.
(5) G is the midpoint of non parallel sides BC.
To find: Ratio of the area of the Quadrilaterals ABFE and EFCD.
Calculation: We know that, ‘Area of a trapezium is half the product of its height and the sum of the parallel sides.’
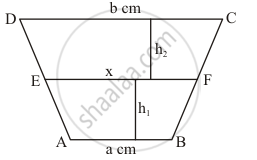
Since, E and F are mid points of AD and BC respectively, so h1 = h2
Area of trapezium ABFE
Area of trapezium ABFE`=1/2 (a + x) h_1 = 1/2 (a + x)h`
Area of trapezium EFCD = `1/2 (b+x)h_2 = 1/2 (b+ x) h`
Area of trapezium ABCD `= 1/2 (a+ b) (h_1 + h_2 ) = (a+b) h`
Now, Area (trap ABCD) = area (trap EFCD) + Area (ABFE)
Therefore,
(a + b) h = `1/2 ( a + x) h + 1/2 (b+x) h`
`⇒ A +b = (a+b)/2 +x`
`⇒x = (a+b)/2`
Thus,
`(Area (ABFE))/(Area (EFCD)) = (a+x)/(b +x) = (a +(a+b)/2)/(b + (a+b)/2)`
`⇒ (Area (ABFE))/(Area (EFCD)) = (3a +b)/(a + 3b)`
APPEARS IN
RELATED QUESTIONS
In the below fig. OCDE is a rectangle inscribed in a quadrant of a circle of radius 10 cm. If
OE = 2√5, find the area of the rectangle.
If AD is a median of a triangle ABC, then prove that triangles ADB and ADC are equal in
area. If G is the mid-point of median AD, prove that ar (Δ BGC) = 2 ar (Δ AGC).
ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects
CD at F.
(i) Prove that ar (ΔADF) = ar (ΔECF)
(ii) If the area of ΔDFB = 3 cm2, find the area of ||gm ABCD.
ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O
intersects AB at P and DC at Q. Prove that ar (Δ POA) = ar (Δ QOC).
In the below fig. X and Y are the mid-points of AC and AB respectively, QP || BC and
CYQ and BXP are straight lines. Prove that ar (Δ ABP) = ar (ΔACQ).
The sides of a rectangular park are in the ratio 4 : 3. If its area is 1728 m2, find
(i) its perimeter
(ii) cost of fencing it at the rate of ₹40 per meter.
Which has the bigger area - one of your footprints or the page of this book?
An engineer who plans to build a compound wall on all sides of a house must find the area of the compound.
Find the area of the following figure by counting squares:
Find the area of the following figure by counting squares:
