Advertisements
Advertisements
Question
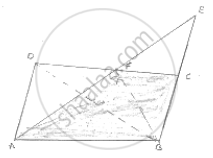
ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects
CD at F.
(i) Prove that ar (ΔADF) = ar (ΔECF)
(ii) If the area of ΔDFB = 3 cm2, find the area of ||gm ABCD.
Solution
In triangles and , ADF ECF we have
∠ADF = ∠ECF [Alternative interior angles, Since || AD BE]
AD = EC [ Since AD = BC = CE ]
And ∠DFA = ∠CFA [vertically opposite angles]
So, by AAS congruence criterion, we have
ΔADF ≅ ECF
⇒ area (ΔADF) = area (ΔECF) and DF = CF.
Now, DF = CF
⇒ BF is a madian in ΔBCD
⇒ area (ΔBCD) =2ar (ΔBDF)
⇒ area (ΔBCD) = 2× 3 cm2 =6cm2
Hence, ar (||gm ABCD) = 2ar (ΔBCD) 2 × 6cm2
=12cm2
APPEARS IN
RELATED QUESTIONS
ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O
intersects AB at P and DC at Q. Prove that ar (Δ POA) = ar (Δ QOC).
D is the mid-point of side BC of ΔABC and E is the mid-point of BD. if O is the mid-point
of AE, prove that ar (ΔBOE) = `1/8` ar (Δ ABC).
ABC is a triangle in which D is the mid-point of BC. E and F are mid-points of DC and AErespectively. IF area of ΔABC is 16 cm2, find the area of ΔDEF.
ABCD is a trapezium with parallel sides AB =a and DC = b. If E and F are mid-points of non-parallel sides AD and BC respectively, then the ratio of areas of quadrilaterals ABFEand EFCD is
Find the area of a rectangle whose length and breadth are 25 m and 16 cm.
Length of a rectangle is 30 m and its breadth is 20 m. Find the increase in its area if its length is increased by 10 m and its breadth is doubled.
If each square on this page is equal to 1 square meter of land, how much land will each of her children get? ________ square m
Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

