Advertisements
Advertisements
Question
ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O
intersects AB at P and DC at Q. Prove that ar (Δ POA) = ar (Δ QOC).
Solution
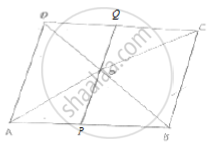
In triangles and , POA QOC we have
∠AOP = ∠COQ [vertically opposite angles]
OA = OC [ Diagonals of a parallelogram bisect each other]
∠PAC = ∠QCA [ AB || DC ; alternative angles ]
So, by ASA congruence criterion, we have
ΔPOA ≅ QOC
Area (ΔPOA) = area (ΔQOC) .
APPEARS IN
RELATED QUESTIONS
In the below Fig, ABC and ABD are two triangles on the base AB. If line segment CD is
bisected by AB at O, show that ar (Δ ABC) = ar (Δ ABD)

ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects
CD at F.
(i) Prove that ar (ΔADF) = ar (ΔECF)
(ii) If the area of ΔDFB = 3 cm2, find the area of ||gm ABCD.
If ABC and BDE are two equilateral triangles such that D is the mid-point of BC, then find ar (ΔABC) : ar (ΔBDE).
PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then find ar (ΔRAS)
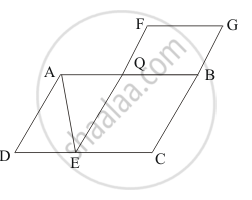
In the given figure, ABCD and FECG are parallelograms equal in area. If ar (ΔAQE) = 12 cm2, then ar (||gm FGBQ) =
The perimeter of a triangle ABC is 37 cm and the ratio between the lengths of its altitudes be 6: 5: 4. Find the lengths of its sides.
Let the sides be x cm, y cm, and (37 - x - y) cm. Also, let the lengths of altitudes be 6a cm, 5a cm, and 4a cm.
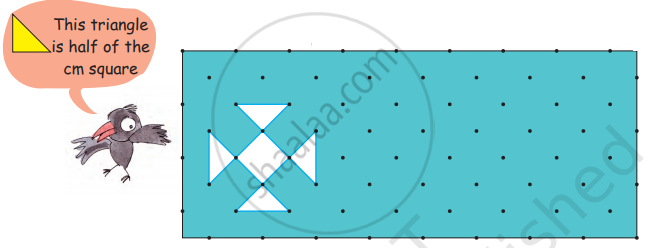
How many tiles like the triangle given here will fit in the white design?
Area of design = ________ square cm
Measure the length of the floor of your classroom in meters. Also, measure the width.
- So how many children can sit in one square meter?
Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

