Advertisements
Advertisements
Question
In the below Fig, ABC and ABD are two triangles on the base AB. If line segment CD is
bisected by AB at O, show that ar (Δ ABC) = ar (Δ ABD)

Solution
Given that CD is bisected at O by AB
To prove: ar (ΔABC) = ar (ΔABD)
Construction: Draw CP ⊥ AB and DQ ⊥ AB
Proof:-
`ar (ΔABC) = 1/2 xx AB xx CP` ........ (1)
`ar (ΔABC) = 1/2 xx AB xx DQ ` ........ (2)
In ∠CPO and ΔDQO
∠CPQ = ΔDQO [Each 90°]
Given that CO = DO
∠COP = ∠DOQ [vertically opposite angles are equal]
Than, ΔCPO ≅ DQO [By AAS condition]
∴ CP = DQ ........... (3) [CP.C.T]
Compare equation (1), (2) and (3)
Area ( ΔABC)a = area of ΔABD
APPEARS IN
RELATED QUESTIONS
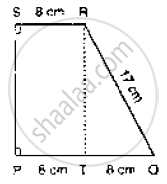
Compute the area of trapezium PQRS is Fig. below.
ABCD is a parallelogram. E is a point on BA such that BE = 2 EA and F is a point on DC
such that DF = 2 FC. Prove that AE CF is a parallelogram whose area is one third of the
area of parallelogram ABCD.
A triangle and a parallelogram are on the same base and between the same parallels. The ratio of the areas of triangle and parallelogram is
The median of a triangle divides it into two ______.
ABCD is a parallelogram. P is any point on CD. If ar (ΔDPA) = 15 cm2 and ar (ΔAPC) = 20 cm2, then ar (ΔAPB) =
The sides of a rectangular park are in the ratio 4 : 3. If its area is 1728 m2, find
(i) its perimeter
(ii) cost of fencing it at the rate of ₹40 per meter.
What will happen to the area of a rectangle, if its length and breadth both are trebled?
Altogether how many squares can be arranged on it?
An engineer who plans to build a compound wall on all sides of a house must find the area of the compound.
A magazine charges Rs 300 per 10 sq cm area for advertising. A company decided to order a half page advertisment. If each page of the magazine is 15 cm × 24 cm, what amount will the company has to pay for it?
