Advertisements
Advertisements
प्रश्न
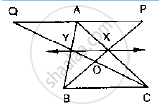
In the below Fig, ABC and ABD are two triangles on the base AB. If line segment CD is
bisected by AB at O, show that ar (Δ ABC) = ar (Δ ABD)

उत्तर
Given that CD is bisected at O by AB
To prove: ar (ΔABC) = ar (ΔABD)
Construction: Draw CP ⊥ AB and DQ ⊥ AB
Proof:-
`ar (ΔABC) = 1/2 xx AB xx CP` ........ (1)
`ar (ΔABC) = 1/2 xx AB xx DQ ` ........ (2)
In ∠CPO and ΔDQO
∠CPQ = ΔDQO [Each 90°]
Given that CO = DO
∠COP = ∠DOQ [vertically opposite angles are equal]
Than, ΔCPO ≅ DQO [By AAS condition]
∴ CP = DQ ........... (3) [CP.C.T]
Compare equation (1), (2) and (3)
Area ( ΔABC)a = area of ΔABD
APPEARS IN
संबंधित प्रश्न
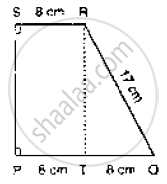
Compute the area of trapezium PQRS is Fig. below.
ABCD is a parallelogram. E is a point on BA such that BE = 2 EA and F is a point on DC
such that DF = 2 FC. Prove that AE CF is a parallelogram whose area is one third of the
area of parallelogram ABCD.
In the below fig. X and Y are the mid-points of AC and AB respectively, QP || BC and
CYQ and BXP are straight lines. Prove that ar (Δ ABP) = ar (ΔACQ).
ABC is a triangle in which D is the mid-point of BC. E and F are mid-points of DC and AErespectively. IF area of ΔABC is 16 cm2, find the area of ΔDEF.
If AD is median of ΔABC and P is a point on AC such that
ar (ΔADP) : ar (ΔABD) = 2 : 3, then ar (Δ PDC) : ar (Δ ABC)
The mid-points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to ______.
By counting squares, estimate the area of the figure.

So the area of piece A = ________ square cm
Is the area of both your footprints the same?
Find the area of the following figure by counting squares:

