Advertisements
Advertisements
प्रश्न
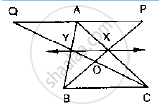
In the below fig. X and Y are the mid-points of AC and AB respectively, QP || BC and
CYQ and BXP are straight lines. Prove that ar (Δ ABP) = ar (ΔACQ).
उत्तर
Since x and y are the midpoint AC and AB respectively
∴ XY ll BC
Clearly, triangles BYC and BXC are on the same base BC and between the same parallels
XY and BC
∴ area (ΔBYC) = area (BXC)
⇒ area (ΔBYC) = ar (ΔBOC) = ar (ΔBXC) - ar (BOC)
⇒ ar (ΔBOY) = ar (ΔCOX)
⇒ ar ( BOY) + ar (XOY) = ar (ΔCOX) + ar (ΔXOY)
⇒ ar (ΔBXY = ar (ΔCXY)
We observe that the quadrilateral XYAP and XYAQ are on the same base XY and between
the same parallel XY and PQ.
∴ area (quad XYAP ) ar (quad XYPA) ....(2)
Adding (1) and (2), we get
ar (ΔBXY) + ar (quad XYAP) = ar (CXY) + ar (quad XYQA)
⇒ ar (ΔABP) = ar (ΔACQ)
APPEARS IN
संबंधित प्रश्न
In the below Fig, ABC and ABD are two triangles on the base AB. If line segment CD is
bisected by AB at O, show that ar (Δ ABC) = ar (Δ ABD)

In below fig., PSDA is a parallelogram in which PQ = QR = RS and AP || BQ || CR. Prove
that ar (Δ PQE) = ar (ΔCFD).
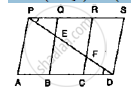
PQRS is a trapezium having PS and QR as parallel sides. A is any point on PQ and B is a point on SR such that AB || QR. If area of ΔPBQ is 17cm2, find the area of ΔASR.
Let ABC be a triangle of area 24 sq. units and PQR be the triangle formed by the mid-points of the sides of Δ ABC. Then the area of ΔPQR is
ABCD is a parallelogram. P is any point on CD. If ar (ΔDPA) = 15 cm2 and ar (ΔAPC) = 20 cm2, then ar (ΔAPB) =
A, B, C, D are mid-points of sides of parallelogram PQRS. If ar (PQRS) = 36 cm2, then ar (ABCD) =
In the given figure, ABCD and FECG are parallelograms equal in area. If ar (ΔAQE) = 12 cm2, then ar (||gm FGBQ) =
The perimeter of a triangle ABC is 37 cm and the ratio between the lengths of its altitudes be 6: 5: 4. Find the lengths of its sides.
Let the sides be x cm, y cm, and (37 - x - y) cm. Also, let the lengths of altitudes be 6a cm, 5a cm, and 4a cm.
What is the area of the rectangle? ________ square cm
Find the area of the following figure by counting squares:

