Advertisements
Advertisements
प्रश्न
In the below fig. X and Y are the mid-points of AC and AB respectively, QP || BC and
CYQ and BXP are straight lines. Prove that ar (Δ ABP) = ar (ΔACQ).
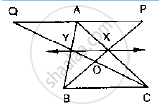
उत्तर
Since x and y are the midpoint AC and AB respectively
∴ XY ll BC
Clearly, triangles BYC and BXC are on the same base BC and between the same parallels
XY and BC
∴ area (ΔBYC) = area (BXC)
⇒ area (ΔBYC) = ar (ΔBOC) = ar (ΔBXC) - ar (BOC)
⇒ ar (ΔBOY) = ar (ΔCOX)
⇒ ar ( BOY) + ar (XOY) = ar (ΔCOX) + ar (ΔXOY)
⇒ ar (ΔBXY = ar (ΔCXY)
We observe that the quadrilateral XYAP and XYAQ are on the same base XY and between
the same parallel XY and PQ.
∴ area (quad XYAP ) ar (quad XYPA) ....(2)
Adding (1) and (2), we get
ar (ΔBXY) + ar (quad XYAP) = ar (CXY) + ar (quad XYQA)
⇒ ar (ΔABP) = ar (ΔACQ)
APPEARS IN
संबंधित प्रश्न
ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O
intersects AB at P and DC at Q. Prove that ar (Δ POA) = ar (Δ QOC).
The mid-points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to ______.
The diagonal of a rectangular board is 1 m and its length is 96 cm. Find the area of the board.
A floor is 40 m long and 15 m broad. It is covered with tiles, each measuring 60 cm by 50 cm. Find the number of tiles required to cover the floor.
The side of a square field is 16 m. What will be increase in its area, if each of its sides is doubled?
The table given below contains some measures of the rectangle. Find the unknown values.
| Length | Breadth | Perimeter | Area |
| ? | 15 cm | 60 cm | ? |
Measure the length of the floor of your classroom in meters. Also, measure the width.
- So how many children can sit in one square meter?
If each square on this page is equal to 1 square meter of land, how much land will each of her children get? ________ square m
How will you decide? Discuss.
Find the area of the following figure by counting squares:

