Question

A, B, C, D are mid-points of sides of parallelogram PQRS. If ar (PQRS) = 36 cm², then ar (ABCD) =

विकल्प

•  24 cm²

•  18cm²

•  30 cm²

•  36 cm²

Answer 1

Given:

(1) PQRS is a parallelogram.

(2) A, B, C, D are the midpoints of the adjacent sides of Parallelogram PQRS.

(3)  `ar ("||"^(gm) PQRS) = 36  cm^2` 

To find:  `AR("||"^(gm) ABCD)`

Calculation:

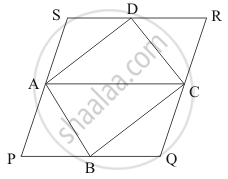
A and C are the midpoints of PS and QR respectively.

`AP = 1/2 SP`

`BP = 1/2 QR`

Now PQRS is a parallelogram which means

     `PS = QR `

`1/2PS = 1/2 QR`

AP = CQ ……..(1)

Also, PS || QR

AP || CQ ……(2)

From 1 and 2 we get that APCQ is a parallelogram.

Since Parallelogram APCQ and ΔABC are on the base AC and between the same parallels AC and PQ.

`∴ ar (ΔABC) = 1/2 ar ("||"^(gm) APCQ)`   ……(3)

Similarly ,

`ar  (ΔADC ) = 1/2 ar ("||"^(gm) ACRS)`   ……(4)

Adding 3 and 4 we get,

`ar (ΔABC ) + ar (ΔADC) = 1/2 ar ("||"^(gm) APCQ) + 1/2 ar("||"^(gm) ACRS)`

                         `ar (ABCD ) = 1/2 (ar ("||"^(gm) APCQ ) + ar ("||"^(gm) ACRS))`

                          `ar (ABCD ) = 1/2 (ar("||"^(gm) PQRS))`

`ar (ABCD ) = 1/2 (36)`

`ar (ABCD) = 18  cm^2`