Advertisements
Advertisements
Question
A, B, C, D are mid-points of sides of parallelogram PQRS. If ar (PQRS) = 36 cm2, then ar (ABCD) =
Options
24 cm2
18cm2
30 cm2
36 cm2
Solution
Given:
(1) PQRS is a parallelogram.
(2) A, B, C, D are the midpoints of the adjacent sides of Parallelogram PQRS.
(3) `ar ("||"^(gm) PQRS) = 36 cm^2`
To find: `AR("||"^(gm) ABCD)`
Calculation:
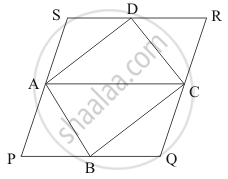
A and C are the midpoints of PS and QR respectively.
`AP = 1/2 SP`
`BP = 1/2 QR`
Now PQRS is a parallelogram which means
`PS = QR `
`1/2PS = 1/2 QR`
AP = CQ ……..(1)
Also, PS || QR
AP || CQ ……(2)
From 1 and 2 we get that APCQ is a parallelogram.
Since Parallelogram APCQ and ΔABC are on the base AC and between the same parallels AC and PQ.
`∴ ar (ΔABC) = 1/2 ar ("||"^(gm) APCQ)` ……(3)
Similarly ,
`ar (ΔADC ) = 1/2 ar ("||"^(gm) ACRS)` ……(4)
Adding 3 and 4 we get,
`ar (ΔABC ) + ar (ΔADC) = 1/2 ar ("||"^(gm) APCQ) + 1/2 ar("||"^(gm) ACRS)`
`ar (ABCD ) = 1/2 (ar ("||"^(gm) APCQ ) + ar ("||"^(gm) ACRS))`
`ar (ABCD ) = 1/2 (ar("||"^(gm) PQRS))`
`ar (ABCD ) = 1/2 (36)`
`ar (ABCD) = 18 cm^2`
APPEARS IN
RELATED QUESTIONS
In the below Fig, ABC and ABD are two triangles on the base AB. If line segment CD is
bisected by AB at O, show that ar (Δ ABC) = ar (Δ ABD)

If P is any point in the interior of a parallelogram ABCD, then prove that area of the
triangle APB is less than half the area of parallelogram.
The diagonal of a rectangular board is 1 m and its length is 96 cm. Find the area of the board.
The sides of a rectangular park are in the ratio 4 : 3. If its area is 1728 m2, find
(i) its perimeter
(ii) cost of fencing it at the rate of ₹40 per meter.
Find the area of a square, whose side is: 4.1 cm.
Each side of a square is 7 m. If its each side be increased by 3 m, what will be the increase in its area.
Find the area and perimeter of the following parallelograms
Find the area and perimeter of the following parallelograms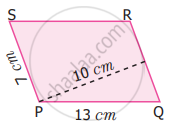
Who had the bigger piece? How much bigger?
Find the area of the following figure by counting squares:

