Advertisements
Advertisements
Question
The area of the figure formed by joining the mid-points of the adjacent sides of a rhombus with diagonals 16 cm and 12 cm is
Options
28 cm2
48 cm2
96 cm2
24 cm2
Advertisements
Solution
Given: Rhombus with diagonals measuring 16cm and 12 cm.
To find: Area of the figure formed by lines joining the midpoints of the adjacent sides.
Calculation: We know that, ‘Area of a rhombus is half the product of their diagonals’.
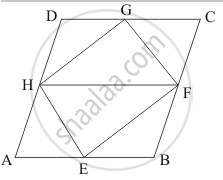
H and F are the midpoints of AD and BC respectively.
`AH = 1/2 AD `
`BE = 1/2 BC`
Now ABCD is a parallelogram which means
`AD = BC `
`1/2AD = 1/2BC`
AH = BF ……..(1)
Also , AD || BC
AH || BF ……(2)
From 1 and 2 we get that ABFH is a parallelogram.
Since Parallelogram FHAB and ΔFHE are on the base FH and between the same parallels HF and AB.
∴` ar (Δ FHE ) = 1/2 ar ( "||"^(gm) FHAB )` ……(3)
Similarly ,
`ar (ΔFHG) = 1/2ar ("||"^(gm) FHDC)` ……(4)
Adding 3 and 4 we get,
`ar (Δ FHE ) + ar (ΔFHG) = 1/2 ar ("||"^(gm) FHAB)+1/2ar("||"^(gm)FHDC)`
`ar (EFGH) = 1/2 (ar("||"^(gm) FHAB ) + ar ("||"^(gm) FHDC))`
`ar (EFGH) = 1/2 (ar("||"^(gm) ABCD))`
`ar (EFGH) = 1/2 (1/2 (16xx12))`
`ar (EFGH) = 1/4 (16 xx 12)`
`ar (EFGH) = 48 cm^2`
APPEARS IN
RELATED QUESTIONS
In the below fig. OCDE is a rectangle inscribed in a quadrant of a circle of radius 10 cm. If
OE = 2√5, find the area of the rectangle.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that:
ar(ΔAPB) × ar(ΔCPD) = ar(ΔAPD) × ar (ΔBPC)
If P is any point in the interior of a parallelogram ABCD, then prove that area of the
triangle APB is less than half the area of parallelogram.
A, B, C, D are mid-points of sides of parallelogram PQRS. If ar (PQRS) = 36 cm2, then ar (ABCD) =
The side of a square field is 16 m. What will be increase in its area, if each of its sides is increased by 4 m?
Parth and Gini bought aam papad (dried mango slice) from a shop. Their pieces looked like these. Both could not make out whose piece was bigger.
- Suggest some ways to find out whose piece is bigger. Discuss
Is the area of your belt the same as the area of the postcard? Why or why not?
Nasreena is a farmer who wants to divide her land equally among her three children — Chumki, Jhumri, and Imran. She wants to divide the land so that each piece of land has one tree. Her land looks like this.
- Can you divide the land equally? Show how you will divide it. Remember each person has to get a tree. Colour each person’s piece of land differently.
Measure the length of the floor of your classroom in meters. Also measure the width.
- If you want to move around easily then how many children do you think should be there in one square meter?
Find the area of the following figure by counting squares:
