Advertisements
Advertisements
Question
If AD is median of ΔABC and P is a point on AC such that
ar (ΔADP) : ar (ΔABD) = 2 : 3, then ar (Δ PDC) : ar (Δ ABC)
Options
1 : 5
1 : 5
1 : 6
3 : 5
Solution
Given: (1) AD is the Median of ΔABC
(2) P is a point on AC such that ar (ΔADP) : ar (ΔABD) = `2/3`
To find: ar (ΔPDC) : ar (ΔABC)
We know that” the medians of the triangle divides the triangle in two two triangles of equal area.”
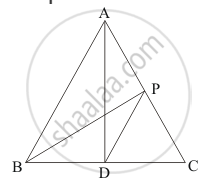
Since AD is the median of ΔABC,
ar (ΔABD) = ar (ΔADC) ……(1)
Also it is given that
ar (ΔADP) : ar (ΔABD) = `2/3` ……(2)
Now,
ar (ΔADC) = ar (ΔADP) + ar (ΔPDC)
ar(ΔADB) = `2/3` ar (ΔADB) + ar (ΔPDC )(from 1 and 2)
ar (ΔPDC ) = `1/3` ar (ΔADB) ..............(3)
ar (ΔABC) = 2ar (ΔADB) ...................(4)
Therefore,
`(ar(ΔPDC))/(ar(ΔABC))= (1/3 ar(ΔADB))/(2ar(ΔADB)`
`(ar(ΔPDC))/(ar(ΔABC))=1/6`
APPEARS IN
RELATED QUESTIONS
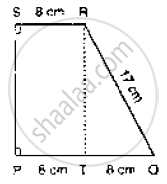
Compute the area of trapezium PQRS is Fig. below.
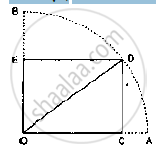
In the below fig. OCDE is a rectangle inscribed in a quadrant of a circle of radius 10 cm. If
OE = 2√5, find the area of the rectangle.
A, B, C, D are mid-points of sides of parallelogram PQRS. If ar (PQRS) = 36 cm2, then ar (ABCD) =
A floor is 40 m long and 15 m broad. It is covered with tiles, each measuring 60 cm by 50 cm. Find the number of tiles required to cover the floor.
Find the area of a rectangle whose length = 24 cm breadth =180 mm
Find the area and perimeter of the following parallelograms
Who had the bigger piece? How much bigger?
The region given in the following figure is measured by taking  as a unit. What is the area of the region?
as a unit. What is the area of the region?
How will you decide? Discuss.
Find the area of the following figure by counting squares:

