Advertisements
Chapters
2: Exponents of Real Numbers
3: Rationalisation
4: Algebraic Identities
5: Factorisation of Algebraic Expressions
6: Factorisation of Polynomials
7: Linear Equations in Two Variables
8: Co-ordinate Geometry
9: Introduction to Euclid’s Geometry
10: Lines and Angles
11: Triangle and its Angles
12: Congruent Triangles
13: Quadrilaterals
▶ 14: Areas of Parallelograms and Triangles
15: Circles
16: Constructions
17: Heron’s Formula
18: Surface Areas and Volume of a Cuboid and Cube
19: Surface Areas and Volume of a Circular Cylinder
20: Surface Areas and Volume of A Right Circular Cone
21: Surface Areas and Volume of a Sphere
22: Tabular Representation of Statistical Data
23: Graphical Representation of Statistical Data
24: Measures of Central Tendency
25: Probability
![RD Sharma solutions for Mathematics [English] Class 9 chapter 14 - Areas of Parallelograms and Triangles RD Sharma solutions for Mathematics [English] Class 9 chapter 14 - Areas of Parallelograms and Triangles - Shaalaa.com](/images/8193647912-mathematics-english-class-9_6:1a030933ece146238cec338f12706a07.jpg)
Advertisements
Solutions for Chapter 14: Areas of Parallelograms and Triangles
Below listed, you can find solutions for Chapter 14 of CBSE RD Sharma for Mathematics [English] Class 9.
RD Sharma solutions for Mathematics [English] Class 9 14 Areas of Parallelograms and Triangles Exercise 14.1 [Page 3]
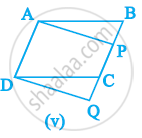
Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
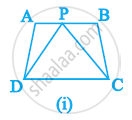
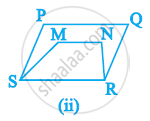
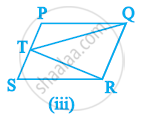
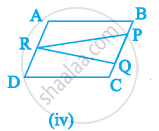

RD Sharma solutions for Mathematics [English] Class 9 14 Areas of Parallelograms and Triangles Exercise 14.2 [Page 15]
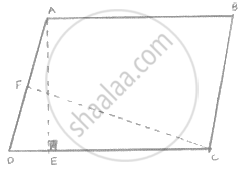
In fig below, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8
cm and CF = 10 cm, find AD.
In Q. No 1, if AD = 6 cm, CF = 10 cm, and AE = 8cm, find AB.
Let ABCD be a parallelogram of area 124 cm2. If E and F are the mid-points of sides AB and
CD respectively, then find the area of parallelogram AEFD.
If ABCD is a parallelogram, then prove that
𝑎𝑟 (Δ𝐴𝐵𝐷) = 𝑎𝑟 (Δ𝐵𝐶𝐷) = 𝑎𝑟 (Δ𝐴𝐵𝐶) = 𝑎𝑟 (Δ𝐴𝐶𝐷) = `1/2` 𝑎𝑟 (||𝑔𝑚 𝐴𝐵𝐶𝐷) .
RD Sharma solutions for Mathematics [English] Class 9 14 Areas of Parallelograms and Triangles Exercise 14.3 [Pages 44 - 48]
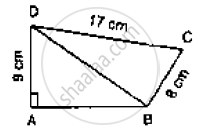
In the below figure, compute the area of quadrilateral ABCD.
In the below figure, PQRS is a square and T and U are respectively, the mid-points of PS
and QR. Find the area of ΔOTS if PQ = 8 cm.

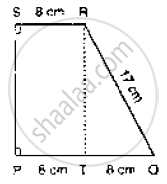
Compute the area of trapezium PQRS is Fig. below.
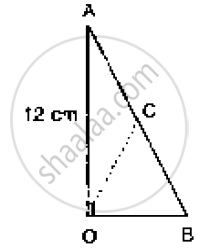
In the below fig. ∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm. Find the area of
ΔAOB.
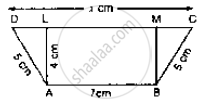
In the below fig. ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm,
and distance between AB and DC is 4cm. Find the value of x and area of trapezium ABCD.
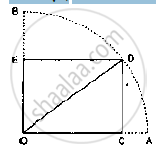
In the below fig. OCDE is a rectangle inscribed in a quadrant of a circle of radius 10 cm. If
OE = 2√5, find the area of the rectangle.
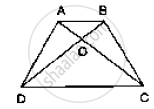
In the below fig. ABCD is a trapezium in which AB || DC. Prove that ar (ΔAOD) =
ar(ΔBOC).
In the given below fig. ABCD, ABFE and CDEF are parallelograms. Prove that ar (ΔADE)
= ar (ΔBCF)
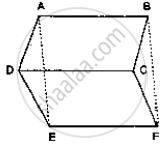
In the below Fig, ABC and ABD are two triangles on the base AB. If line segment CD is
bisected by AB at O, show that ar (Δ ABC) = ar (Δ ABD)

If AD is a median of a triangle ABC, then prove that triangles ADB and ADC are equal in
area. If G is the mid-point of median AD, prove that ar (Δ BGC) = 2 ar (Δ AGC).
A point D is taken on the side BC of a ΔABC such that BD = 2DC. Prove that ar(Δ ABD) =
2ar (ΔADC).
ABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove
that: (1) ar (ΔADO) = ar (ΔCDO) (2) ar (ΔABP) = ar (ΔCBP)
ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects
CD at F.
(i) Prove that ar (ΔADF) = ar (ΔECF)
(ii) If the area of ΔDFB = 3 cm2, find the area of ||gm ABCD.
ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O
intersects AB at P and DC at Q. Prove that ar (Δ POA) = ar (Δ QOC).
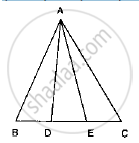
In the below fig. D and E are two points on BC such that BD = DE = EC. Show that ar
(ΔABD) = ar (ΔADE) = ar (ΔAEC).
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that:
ar(ΔAPB) × ar(ΔCPD) = ar(ΔAPD) × ar (ΔBPC)
If P is any point in the interior of a parallelogram ABCD, then prove that area of the
triangle APB is less than half the area of parallelogram.
ABCD is a parallelogram. E is a point on BA such that BE = 2 EA and F is a point on DC
such that DF = 2 FC. Prove that AE CF is a parallelogram whose area is one third of the
area of parallelogram ABCD.
In a ΔABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point
of AP. Prove that :
(1) ar (Δ PBQ) = ar (Δ ARC)
(2) ar (Δ PRQ) =`1/2`ar (Δ ARC)
(3) ar (Δ RQC) =`3/8` ar (Δ ABC) .
ABCD is a parallelogram, G is the point on AB such that AG = 2 GB, E is a point of DC
such that CE = 2DE and F is the point of BC such that BF = 2FC. Prove that:
(1) ar ( ADEG) = ar (GBCD)
(2) ar (ΔEGB) = `1/6` ar (ABCD)
(3) ar (ΔEFC) = `1/2` ar (ΔEBF)
(4) ar (ΔEBG) = ar (ΔEFC)
(5)ΔFind what portion of the area of parallelogram is the area of EFG.
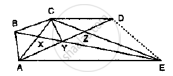
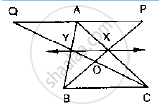
In Fig. below, CD || AE and CY || BA.
(i) Name a triangle equal in area of ΔCBX
(ii) Prove that ar (Δ ZDE) = ar (ΔCZA)
(iii) Prove that ar (BCZY) = ar (Δ EDZ)
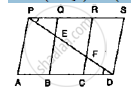
In below fig., PSDA is a parallelogram in which PQ = QR = RS and AP || BQ || CR. Prove
that ar (Δ PQE) = ar (ΔCFD).
In the below fig. ABCD is a trapezium in which AB || DC and DC = 40 cm and AB = 60
cm. If X and Y are respectively, the mid-points of AD and BC, prove that:
(i) XY = 50 cm
(ii) DCYX is a trapezium
(iii) ar (trap. DCYX) =`9/11`ar (trap. (XYBA))
D is the mid-point of side BC of ΔABC and E is the mid-point of BD. if O is the mid-point
of AE, prove that ar (ΔBOE) = `1/8` ar (Δ ABC).
In the below fig. X and Y are the mid-points of AC and AB respectively, QP || BC and
CYQ and BXP are straight lines. Prove that ar (Δ ABP) = ar (ΔACQ).
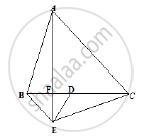
In the below fig. ABCD and AEFD are two parallelograms. Prove that
(1) PE = FQ
(2) ar (Δ APE) : ar (ΔPFA) = ar Δ(QFD) : ar (Δ PFD)
(3) ar (ΔPEA) = ar (ΔQFD)
In the below figure, ABCD is parallelogram. O is any point on AC. PQ || AB and LM ||
AD. Prove that ar (||gm DLOP) = ar (||gm BMOQ)
In a ΔABC, if L and M are points on AB and AC respectively such that LM || BC. Prove
that:
(1) ar (ΔLCM ) = ar (ΔLBM )
(2) ar (ΔLBC) = ar (ΔMBC)
(3) ar (ΔABM) ar (ΔACL)
(4) ar (ΔLOB) ar (ΔMOC)
In Fig. below, ABC and BDE are two equilateral triangles such that D is the mid-point of
BC. AE intersects BC in F. Prove that
(1) ar (Δ BDE) = `1/2` ar (ΔABC)
(2) Area ( ΔBDE) `= 1/2 ` ar (ΔBAE)
(3) ar (BEF) = ar (ΔAFD)
(4) area (Δ ABC) = 2 area (ΔBEC)
(5) ar (ΔFED) `= 1/8` ar (ΔAFC)
(6) ar (Δ BFE) = 2 ar (ΔEFD)
In the following figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:-
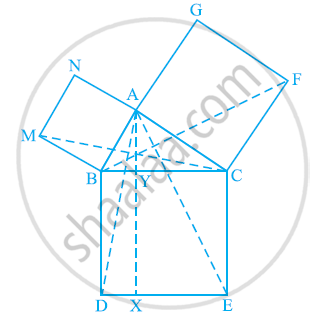
(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar(MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar (CYXE) = ar(ACFG)
(vii) ar (BCED) = ar(ABMN) + ar(ACFG)
Note : Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.
RD Sharma solutions for Mathematics [English] Class 9 14 Areas of Parallelograms and Triangles Exercise 14.4 [Pages 59 - 60]
If ABC and BDE are two equilateral triangles such that D is the mid-point of BC, then find ar (ΔABC) : ar (ΔBDE).
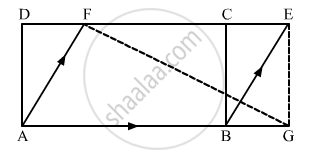
In the given figure, ABCD is a rectangle in which CD = 6 cm, AD = 8 cm. Find the area of parallelogram CDEF.

In the given figure, find the area of ΔGEF.
In the given figure, ABCD is a rectangle with sides AB = 10 cm and AD = 5 cm. Find the area of ΔEFG.
PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then find ar (ΔRAS)
In square ABCD, P and Q are mid-point of AB and CD respectively. If AB = 8cm and PQand BD intersect at O, then find area of ΔOPB.
ABC is a triangle in which D is the mid-point of BC. E and F are mid-points of DC and AErespectively. IF area of ΔABC is 16 cm2, find the area of ΔDEF.
PQRS is a trapezium having PS and QR as parallel sides. A is any point on PQ and B is a point on SR such that AB || QR. If area of ΔPBQ is 17cm2, find the area of ΔASR.
ABCD is a parallelogram. P is the mid-point of AB. BD and CP intersect at Q such that CQ: QP = 3.1. If ar (ΔPBQ) = 10cm2, find the area of parallelogram ABCD.
P is any point on base BC of ΔABC and D is the mid-point of BC. DE is drawn parallel toPA to meet AC at E. If ar (ΔABC) = 12 cm2, then find area of ΔEPC.
RD Sharma solutions for Mathematics [English] Class 9 14 Areas of Parallelograms and Triangles Exercise 14.5 [Pages 60 - 62]
Two parallelograms are on the same base and between the same parallels. The ratio of their areas is
1 : 2
2 : 1
1 : 1
3 : 1
A triangle and a parallelogram are on the same base and between the same parallels. The ratio of the areas of triangle and parallelogram is
1 : 1
1 : 2
2 : 1
1 : 3
Let ABC be a triangle of area 24 sq. units and PQR be the triangle formed by the mid-points of the sides of Δ ABC. Then the area of ΔPQR is
12 sq. units
6 sq. units
4 sq. units
3 sq. units
The median of a triangle divides it into two ______.
triangles of equal area
congruent triangles
right triangles
isosceles triangles
In a ΔABC, D, E, F are the mid-points of sides BC, CA and AB respectively. If ar (ΔABC) = 16cm2, then ar (trapezium FBCE) =
4 cm2
8 cm2
12 cm2
10 cm2
ABCD is a parallelogram. P is any point on CD. If ar (ΔDPA) = 15 cm2 and ar (ΔAPC) = 20 cm2, then ar (ΔAPB) =
15 cm2
20 cm2
35 cm2
30 cm2
The area of the figure formed by joining the mid-points of the adjacent sides of a rhombus with diagonals 16 cm and 12 cm is
28 cm2
48 cm2
96 cm2
24 cm2
A, B, C, D are mid-points of sides of parallelogram PQRS. If ar (PQRS) = 36 cm2, then ar (ABCD) =
24 cm2
18cm2
30 cm2
36 cm2
The figure obtained by joining the mid-points of the adjacent sides of a rectangle of sides 8 cm and 6 cm is ______.
a rhombus of area 24 cm2
a rectangle of area 24 cm2
a square of area 26 cm2
a trapezium of area 14 cm2
If AD is median of ΔABC and P is a point on AC such that
ar (ΔADP) : ar (ΔABD) = 2 : 3, then ar (Δ PDC) : ar (Δ ABC)
1 : 5
1 : 5
1 : 6
3 : 5
Medians of ΔABC intersect at G. If ar (ΔABC) = 27 cm2, then ar (ΔBGC) =
6 cm2
9 cm2
12 cm2
18 cm2
In a ΔABC if D and E are mid-points of BC and AD respectively such that ar (ΔAEC) = 4cm2, then ar (ΔBEC) =
4 cm2
6 cm2
8 cm2
12 cm2
In the given figure, ABCD is a parallelogram. If AB = 12 cm, AE = 7.5 cm, CF = 15 cm, then AD =

In the given figure, PQRS is a parallelogram. If X and Y are mid-points of PQ and SRrespectively and diagonal Q is joined. The ratio ar (||gm XQRY) : ar (ΔQSR) =
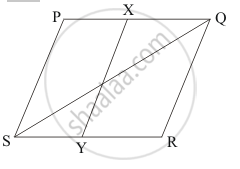
1 : 4
2 : 1
1 : 2
1 : 1
Diagonal AC and BD of trapezium ABCD, in which AB || DC, intersect each other at O. The triangle which is equal in area of ΔAOD is
ΔAOB
ΔBOC
ΔDOC
ΔADC
ABCD is a trapezium in which AB || DC. If ar (ΔABD) = 24 cm2 and AB = 8 cm, then height of ΔABC is
3 cm
4 cm
6 cm
8 cm
ABCD is a trapezium with parallel sides AB =a and DC = b. If E and F are mid-points of non-parallel sides AD and BC respectively, then the ratio of areas of quadrilaterals ABFEand EFCD is
a : b
(a + 3b): (3a + b)
(3a + b) : (a + 3b)
(2a + b) : (3a + b)
ABCD is a rectangle with O as any point in its interior. If ar (ΔAOD) = 3 cm2 and ar (ΔABOC) = 6 cm2, then area of rectangle ABCD is
9 cm2
12 cm2
15 cm2
18 cm2
The mid-points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to ______.
`1/2` ar (ABC)
- `1/3` ar (ABC)
- `1/4` ar (ABC)
- ar (ABC)
In the given figure, ABCD and FECG are parallelograms equal in area. If ar (ΔAQE) = 12 cm2, then ar (||gm FGBQ) =
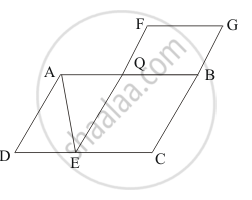
12 cm2
20 cm2
24 cm2
36 cm2
Solutions for 14: Areas of Parallelograms and Triangles
![RD Sharma solutions for Mathematics [English] Class 9 chapter 14 - Areas of Parallelograms and Triangles RD Sharma solutions for Mathematics [English] Class 9 chapter 14 - Areas of Parallelograms and Triangles - Shaalaa.com](/images/8193647912-mathematics-english-class-9_6:1a030933ece146238cec338f12706a07.jpg)
RD Sharma solutions for Mathematics [English] Class 9 chapter 14 - Areas of Parallelograms and Triangles
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 9 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. RD Sharma solutions for Mathematics Mathematics [English] Class 9 CBSE 14 (Areas of Parallelograms and Triangles) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. RD Sharma textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 9 chapter 14 Areas of Parallelograms and Triangles are Corollary: Triangles on the same base and between the same parallels are equal in area., Corollary: A rectangle and a parallelogram on the same base and between the same parallels are equal in area., Theorem: Parallelograms on the Same Base and Between the Same Parallels., Concept of Area.
Using RD Sharma Mathematics [English] Class 9 solutions Areas of Parallelograms and Triangles exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in RD Sharma Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 9 students prefer RD Sharma Textbook Solutions to score more in exams.
Get the free view of Chapter 14, Areas of Parallelograms and Triangles Mathematics [English] Class 9 additional questions for Mathematics Mathematics [English] Class 9 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
