Advertisements
Advertisements
Question
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that:
ar(ΔAPB) × ar(ΔCPD) = ar(ΔAPD) × ar (ΔBPC)
Solution
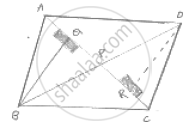
Construction: Draw BQ ⊥ AC and DR ⊥ AC
Proof:
L.H.S
= ar (Δ APB ) × ar (ΔCP)
= `1/2[ ( AP xx BQ )] xx (1/2 xx PC xx DR)`
=`( 1/2 xx PC xx BQ )xx (1/2 xx AP xx DR)`
= ar (Δ BPC ) × ar (APR)
= RHS
∴ LHS = RHS
Hence proved.
APPEARS IN
RELATED QUESTIONS
If ABCD is a parallelogram, then prove that
𝑎𝑟 (Δ𝐴𝐵𝐷) = 𝑎𝑟 (Δ𝐵𝐶𝐷) = 𝑎𝑟 (Δ𝐴𝐵𝐶) = 𝑎𝑟 (Δ𝐴𝐶𝐷) = `1/2` 𝑎𝑟 (||𝑔𝑚 𝐴𝐵𝐶𝐷) .
In the below Fig, ABC and ABD are two triangles on the base AB. If line segment CD is
bisected by AB at O, show that ar (Δ ABC) = ar (Δ ABD)

The mid-points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to ______.
Find the area of a square, whose side is: 4.5 cm.
Parth and Gini bought aam papad (dried mango slice) from a shop. Their pieces looked like these. Both could not make out whose piece was bigger.
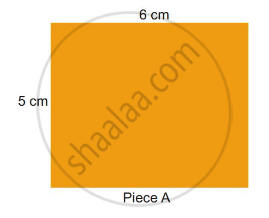
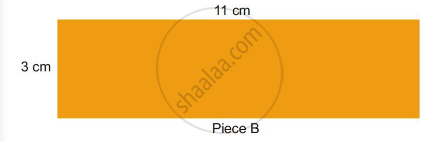
- Suggest some ways to find out whose piece is bigger. Discuss
Altogether how many squares can be arranged on it?
Find all the possible dimensions (in natural numbers) of a rectangle with a perimeter 36 cm and find their areas.
How will you decide? Discuss.
Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

