Advertisements
Advertisements
प्रश्न
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that:
ar(ΔAPB) × ar(ΔCPD) = ar(ΔAPD) × ar (ΔBPC)
Advertisements
उत्तर
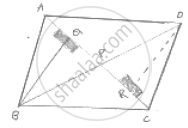
Construction: Draw BQ ⊥ AC and DR ⊥ AC
Proof:
L.H.S
= ar (Δ APB ) × ar (ΔCP)
= `1/2[ ( AP xx BQ )] xx (1/2 xx PC xx DR)`
=`( 1/2 xx PC xx BQ )xx (1/2 xx AP xx DR)`
= ar (Δ BPC ) × ar (APR)
= RHS
∴ LHS = RHS
Hence proved.
APPEARS IN
संबंधित प्रश्न
The mid-points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to ______.
The diagonal of a rectangular board is 1 m and its length is 96 cm. Find the area of the board.
By counting squares, estimate the area of the figure.
How many tiles like the triangle given here will fit in the white design?
Area of design = ________ square cm
The King was very happy with carpenters Cheggu and Anar. They had made a very big and beautiful bed for him. So as gifts the king wanted to give some land to Cheggu, and some gold to Anar. Cheggu was happy. He took 100 meters of wire and tried to make different rectangles.
He made a 10 m × 40 m rectangle. Its area was 400 square meters. So he next made a 30 m × 20 m rectangle.
- What other rectangles can he make with 100 meters of wire? Discuss which of these rectangles will have the biggest area.
In the following figure, the area of parallelogram ABCD is ______.
Find all the possible dimensions (in natural numbers) of a rectangle with a perimeter 36 cm and find their areas.
Find the area of the following figure by counting squares:
Find the area of the following figure by counting squares:
Find the area of the following figure by counting squares:
