Advertisements
Advertisements
प्रश्न
If P is any point in the interior of a parallelogram ABCD, then prove that area of the
triangle APB is less than half the area of parallelogram.
उत्तर
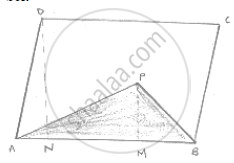
Draw DN ⊥ AB and PM ⊥ AB.
Now,
`Area (ΙΙ^(gm) ABCD) = AB xx DN , ar (ΔAPB ) = 1/2 (AB xx PM)`
Now , PM < DN
⇒ `AB xx PM < AB xx DN`
⇒ ` 1/2 (AB xx PM) < 1/2 (AB xx DN)`
⇒ `Area ( ΔAPB ) <1/2 ar ( Parragram ABCD)`
APPEARS IN
संबंधित प्रश्न
In Q. No 1, if AD = 6 cm, CF = 10 cm, and AE = 8cm, find AB.
In the given figure, find the area of ΔGEF.
A triangle and a parallelogram are on the same base and between the same parallels. The ratio of the areas of triangle and parallelogram is
Let ABC be a triangle of area 24 sq. units and PQR be the triangle formed by the mid-points of the sides of Δ ABC. Then the area of ΔPQR is
The area of the figure formed by joining the mid-points of the adjacent sides of a rhombus with diagonals 16 cm and 12 cm is
A, B, C, D are mid-points of sides of parallelogram PQRS. If ar (PQRS) = 36 cm2, then ar (ABCD) =
Medians of ΔABC intersect at G. If ar (ΔABC) = 27 cm2, then ar (ΔBGC) =
In the given figure, ABCD is a parallelogram. If AB = 12 cm, AE = 7.5 cm, CF = 15 cm, then AD =

Look at the table. If you were to write the area of each of these which column would you choose? Make a (✓).
| Square cm |
Square meter |
Square km |
|
| Handkerchief | ✓ | ||
| Sari | |||
| Page of your book | |||
| School land | |||
| Total land of a city | |||
| Door of your classroom | |||
| Chair seat | |||
| Blackboard | |||
| Indian flag | |||
| Land over which a river flows |
Find all the possible dimensions (in natural numbers) of a rectangle with a perimeter 36 cm and find their areas.
