Advertisements
Advertisements
Question
If P is any point in the interior of a parallelogram ABCD, then prove that area of the
triangle APB is less than half the area of parallelogram.
Solution
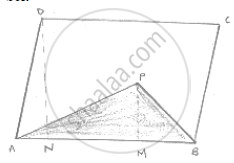
Draw DN ⊥ AB and PM ⊥ AB.
Now,
`Area (ΙΙ^(gm) ABCD) = AB xx DN , ar (ΔAPB ) = 1/2 (AB xx PM)`
Now , PM < DN
⇒ `AB xx PM < AB xx DN`
⇒ ` 1/2 (AB xx PM) < 1/2 (AB xx DN)`
⇒ `Area ( ΔAPB ) <1/2 ar ( Parragram ABCD)`
APPEARS IN
RELATED QUESTIONS
In Q. No 1, if AD = 6 cm, CF = 10 cm, and AE = 8cm, find AB.
Let ABCD be a parallelogram of area 124 cm2. If E and F are the mid-points of sides AB and
CD respectively, then find the area of parallelogram AEFD.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that:
ar(ΔAPB) × ar(ΔCPD) = ar(ΔAPD) × ar (ΔBPC)
If AD is a median of a triangle ABC, then prove that triangles ADB and ADC are equal in
area. If G is the mid-point of median AD, prove that ar (Δ BGC) = 2 ar (Δ AGC).
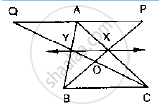
In the below fig. X and Y are the mid-points of AC and AB respectively, QP || BC and
CYQ and BXP are straight lines. Prove that ar (Δ ABP) = ar (ΔACQ).
PQRS is a trapezium having PS and QR as parallel sides. A is any point on PQ and B is a point on SR such that AB || QR. If area of ΔPBQ is 17cm2, find the area of ΔASR.
Find the area of a square, whose side is: 4.1 cm.
Is the area of the blue shape more than the area of the yellow shape? Why?

Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- A shopkeeper has 204 eggs. He puts them in egg trays. Each tray has 12 eggs.
a) How many more eggs will he need? b) How many fresh eggs does he sell? c) How many egg trays does he need?
Find the area of the following figure by counting squares:

