Advertisements
Advertisements
Question
The mid-points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to ______.
Options
`1/2` ar (ABC)
- `1/3` ar (ABC)
- `1/4` ar (ABC)
- ar (ABC)
Solution
The mid-points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to `underlinebb(1/2 ar (ABC))`.
Explanation:
Given: ABCD is a triangle.
Mid points of the sides of ΔABC with any of the vertices forms a parallelogram.
To find: Area of the parallelogram
Calculation: We know that, Area of a parallelogram = base × height
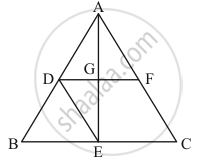
Hence area of || gm DECF = EC × EG
area of || gm DECF = EC × EG
area of || gm DECF = `1/2 BC xx 1/2 AE` ...(E is the midpoint of BC)
area of || gm DECF = `1/2(1/2BC xx AE)`
area of || gm DECF = `1/2(ar ( ΔABC) `
APPEARS IN
RELATED QUESTIONS
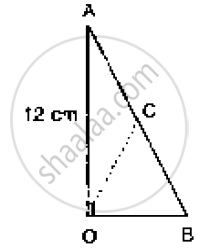
In the below fig. ∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm. Find the area of
ΔAOB.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that:
ar(ΔAPB) × ar(ΔCPD) = ar(ΔAPD) × ar (ΔBPC)
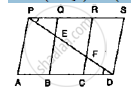
In below fig., PSDA is a parallelogram in which PQ = QR = RS and AP || BQ || CR. Prove
that ar (Δ PQE) = ar (ΔCFD).
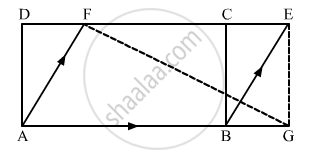
In the given figure, ABCD is a rectangle with sides AB = 10 cm and AD = 5 cm. Find the area of ΔEFG.
Medians of ΔABC intersect at G. If ar (ΔABC) = 27 cm2, then ar (ΔBGC) =
Find the area of a rectangle whose length = 3.6 m breadth = 90 cm
Find the area of a square, whose side is: 7.2 cm.
Each side of a square is 7 m. If its each side be increased by 3 m, what will be the increase in its area.
Altogether how many squares can be arranged on it?
This stamp has an area of 4 square cm. Guess how many such stamps will cover this big rectangle.

