Advertisements
Advertisements
Question
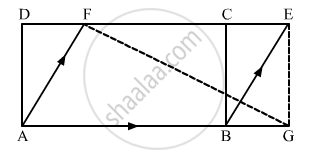
In the given figure, ABCD is a rectangle with sides AB = 10 cm and AD = 5 cm. Find the area of ΔEFG.
Solution
Given: (1) ABCD is a rectangle.
(2) AB = 10 cm
(3) AD = 5cm
To find: Area of ΔEGF.
Calculation: We know that,
Area of Rectangle = base × height
If a triangle and a parallelogram are on the same base and between the same parallels, the area of the triangle is equal to half of the parallelogram

Here we can see that Rectangle ABCD and triangle GEF are between the same base and same parallels.
Hence,
Area of ΔGEF = `1/2` Area of Rectangle ABCD
`= 1/2 xx AD xx CD`
`= 1/2 xx 10 xx 5 `
= 25 cm2
Hence we get the result as Area of ΔGEF = 25 cm2
APPEARS IN
RELATED QUESTIONS
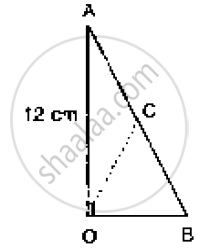
In the below fig. ∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm. Find the area of
ΔAOB.
In the below Fig, ABC and ABD are two triangles on the base AB. If line segment CD is
bisected by AB at O, show that ar (Δ ABC) = ar (Δ ABD)

The mid-points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to ______.
The sides of a rectangular park are in the ratio 4 : 3. If its area is 1728 m2, find
(i) its perimeter
(ii) cost of fencing it at the rate of ₹40 per meter.
The side of a square field is 16 m. What will be increase in its area, if each of its sides is increased by 4 m?
Is the area of the blue shape more than the area of the yellow shape? Why?

So the area of piece A = ________ square cm
What is the area of the rectangle? ________ square cm
Whose footprint is larger - yours or your friend’s?
Find the area of the following figure by counting squares:

