Advertisements
Advertisements
Question
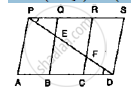
In below fig., PSDA is a parallelogram in which PQ = QR = RS and AP || BQ || CR. Prove
that ar (Δ PQE) = ar (ΔCFD).
Solution
Given that PSDA is a parallelogram
Since, AP || BQ ||CR || DS and AD || PS
∴PQ = CD .....(1)
In ΔBED,C is the midpoint of BD and CF || BE
∴ F is the midpoint of ED
⇒ EF = PE
similarly
EF = FD
∴ PE = FD ........ (2)
In Δ SPQE and CFD , WE have
PE = FD
∠EDQ = ∠FDC, [Alternative angles]
And PQ = CD
So by SAS congruence criterion, we have . ΔPQE ≅ ΔDCF .
APPEARS IN
RELATED QUESTIONS
In fig below, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8
cm and CF = 10 cm, find AD.
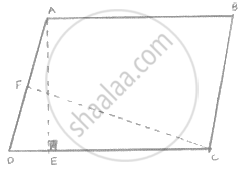
In Q. No 1, if AD = 6 cm, CF = 10 cm, and AE = 8cm, find AB.
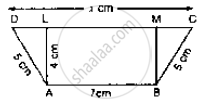
In the below fig. ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm,
and distance between AB and DC is 4cm. Find the value of x and area of trapezium ABCD.
ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects
CD at F.
(i) Prove that ar (ΔADF) = ar (ΔECF)
(ii) If the area of ΔDFB = 3 cm2, find the area of ||gm ABCD.
ABCD is a trapezium with parallel sides AB =a and DC = b. If E and F are mid-points of non-parallel sides AD and BC respectively, then the ratio of areas of quadrilaterals ABFEand EFCD is
Find the area of a rectangle whose length and breadth are 25 m and 16 cm.
A floor is 40 m long and 15 m broad. It is covered with tiles, each measuring 60 cm by 50 cm. Find the number of tiles required to cover the floor.
Find the area and perimeter of the following parallelograms
An engineer who plans to build a compound wall on all sides of a house must find the area of the compound.
Find the area of the following figure by counting squares:

