Advertisements
Advertisements
Question
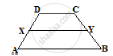
In the below fig. ABCD is a trapezium in which AB || DC and DC = 40 cm and AB = 60
cm. If X and Y are respectively, the mid-points of AD and BC, prove that:
(i) XY = 50 cm
(ii) DCYX is a trapezium
(iii) ar (trap. DCYX) =`9/11`ar (trap. (XYBA))
Solution
(1) Join DY and produce it to meet AB produced at P
In Δ' s BYP and CYDwe have
∠BYP =(∠CYD) [Vertical opposite angles]
∠DCY ∠ (∠CYD) [∴ DC || AP ]
And By = CY
So, by ASA congruence criterion, we have
Δ BYP ≅ CYD
⇒ DY =YP and DC = BP
⇒ y is the midpoint of DP
Also, x is the midpoint of AD
∴ XY || AP and XY = `1/2`AD
⇒ `xy = 1/2 ( AB + BD)`
⇒ `xy = 1/2 (BA + DC )⇒ xy = 1/2 ( 60 + 40 )`
(2) We have
XY || AP
⇒ XY || AB and AB || DC [As proved above]
⇒ XY || DC
⇒ DCY is a trapezium
(3) Since x and y are the midpoint of DA and CB respectively
∴Trapezium DCXY and ABYX are of the same height say hm
Now
ar (Trap DCXY) =`1/2`(DC + XY) × h
`= 1/2 (50 + 40) hcm^2 = 45 hcm^2`
⇒ `ar (trap ABXY) = 1/2 (AB + XY) xx h = 1/2 (60 + 50) hm^3 `
⇒`ar (trap ABXY) = 1/2 (AB + XY) xx h = 1/2 (60 + 50) hm^2 `
= 55 cm2
` (ar trap (YX))/(ar trap (ABYX)) = (45h )/ (55h)= 9 /11 `
⇒ ar (trap DCYX) =`9/11` ar (trap ABXY)
APPEARS IN
RELATED QUESTIONS
Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
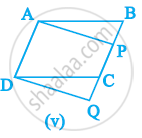

In the below figure, compute the area of quadrilateral ABCD.
In the below figure, PQRS is a square and T and U are respectively, the mid-points of PS
and QR. Find the area of ΔOTS if PQ = 8 cm.

In the below fig. ABCD is a trapezium in which AB || DC. Prove that ar (ΔAOD) =
ar(ΔBOC).
In Fig. below, CD || AE and CY || BA.
(i) Name a triangle equal in area of ΔCBX
(ii) Prove that ar (Δ ZDE) = ar (ΔCZA)
(iii) Prove that ar (BCZY) = ar (Δ EDZ)
In the below figure, ABCD is parallelogram. O is any point on AC. PQ || AB and LM ||
AD. Prove that ar (||gm DLOP) = ar (||gm BMOQ)
If bisectors of ∠A and ∠B of a quadrilateral ABCD meet at O, then ∠AOB is
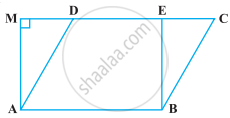
In the following figure, if parallelogram ABCD and rectangle ABEM are of equal area, then ______.
ABCD is a quadrilateral whose diagonal AC divides it into two parts, equal in area, then ABCD ______.
