Advertisements
Advertisements
Question
In Fig. below, CD || AE and CY || BA.
(i) Name a triangle equal in area of ΔCBX
(ii) Prove that ar (Δ ZDE) = ar (ΔCZA)
(iii) Prove that ar (BCZY) = ar (Δ EDZ)
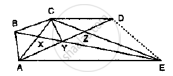
Solution
Since, ΔBCA and ΔBYAare on the same base BA and between same parallels BA and CY Then area (ΔBCA) = ar (BYA)
⇒ ar (Δ CBX) + ar (Δ BXA) = ar (Δ BXA) + ar (ΔAXY)
⇒ ar (Δ CBX) = ar (Δ AXY) ........ (1)
Since, ΔACE and ΔADE are on the same base AE and between same parallels CD and AE
Then, ar (ΔACE) ar (ΔADE)
⇒ (ΔCLA) + ar (ΔAZE) = ar (ΔAZE) + ar (ΔDZE)
⇒ ar (ΔCZA) = (ΔDZE) ........ (2)
Since ΔCBY and ΔCAY are on the same base CY and between same parallels
BA and CY
Then ar (ΔCBY) ar (ΔCAY )
Adding ar (ΔCYG) on both sides, we get
⇒ ar (ΔCBX) + ar (ΔCYZ) = ar (ΔCAY) + ar (ΔCYZ)
⇒ ar (BCZX) = ar (Δ CZA) ......... (3)
Compare equation (2) and (3)
ar (BCZY) = ar (ΔDZE)
APPEARS IN
RELATED QUESTIONS
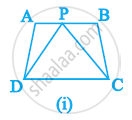
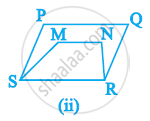
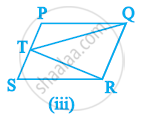
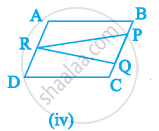
Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
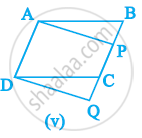

In the below figure, compute the area of quadrilateral ABCD.
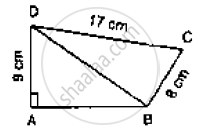
In the below figure, PQRS is a square and T and U are respectively, the mid-points of PS
and QR. Find the area of ΔOTS if PQ = 8 cm.

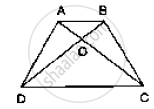
In the below fig. ABCD is a trapezium in which AB || DC. Prove that ar (ΔAOD) =
ar(ΔBOC).
In the below fig. ABCD is a trapezium in which AB || DC and DC = 40 cm and AB = 60
cm. If X and Y are respectively, the mid-points of AD and BC, prove that:
(i) XY = 50 cm
(ii) DCYX is a trapezium
(iii) ar (trap. DCYX) =`9/11`ar (trap. (XYBA))
In the below figure, ABCD is parallelogram. O is any point on AC. PQ || AB and LM ||
AD. Prove that ar (||gm DLOP) = ar (||gm BMOQ)
If bisectors of ∠A and ∠B of a quadrilateral ABCD meet at O, then ∠AOB is
In the following figure, if parallelogram ABCD and rectangle ABEM are of equal area, then ______.
ABCD is a quadrilateral whose diagonal AC divides it into two parts, equal in area, then ABCD ______.
