Advertisements
Advertisements
प्रश्न
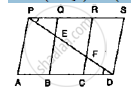
In below fig., PSDA is a parallelogram in which PQ = QR = RS and AP || BQ || CR. Prove
that ar (Δ PQE) = ar (ΔCFD).
उत्तर
Given that PSDA is a parallelogram
Since, AP || BQ ||CR || DS and AD || PS
∴PQ = CD .....(1)
In ΔBED,C is the midpoint of BD and CF || BE
∴ F is the midpoint of ED
⇒ EF = PE
similarly
EF = FD
∴ PE = FD ........ (2)
In Δ SPQE and CFD , WE have
PE = FD
∠EDQ = ∠FDC, [Alternative angles]
And PQ = CD
So by SAS congruence criterion, we have . ΔPQE ≅ ΔDCF .
APPEARS IN
संबंधित प्रश्न
Let ABCD be a parallelogram of area 124 cm2. If E and F are the mid-points of sides AB and
CD respectively, then find the area of parallelogram AEFD.
ABCD is a parallelogram. E is a point on BA such that BE = 2 EA and F is a point on DC
such that DF = 2 FC. Prove that AE CF is a parallelogram whose area is one third of the
area of parallelogram ABCD.
In a ΔABC, D, E, F are the mid-points of sides BC, CA and AB respectively. If ar (ΔABC) = 16cm2, then ar (trapezium FBCE) =
In the given figure, ABCD and FECG are parallelograms equal in area. If ar (ΔAQE) = 12 cm2, then ar (||gm FGBQ) =
The medians of a triangle ABC intersect each other at point G. If one of its medians is AD,
prove that:
(i) Area ( ΔABD ) = 3 x Area ( ΔBGD )
(ii) Area ( ΔACD ) = 3 x Area ( ΔCGD )
(iii) Area ( ΔBGC ) = `1/3` x Area ( ΔABC ).
Find the area of a square, whose side is: 4.1 cm.
What is the area of the rectangle? ________ square cm
Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- 352 children from a school went on a camping trip. Each tent had a group of 4 children.
a) How many children did each tent have? b) How many tents do they need? c) How many children in all are in the school?
How will you decide? Discuss.
Find the area of the following figure by counting squares:

