Advertisements
Advertisements
Question
In Fig. below, ABC and BDE are two equilateral triangles such that D is the mid-point of
BC. AE intersects BC in F. Prove that
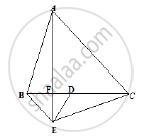
(1) ar (Δ BDE) = `1/2` ar (ΔABC)
(2) Area ( ΔBDE) `= 1/2 ` ar (ΔBAE)
(3) ar (BEF) = ar (ΔAFD)
(4) area (Δ ABC) = 2 area (ΔBEC)
(5) ar (ΔFED) `= 1/8` ar (ΔAFC)
(6) ar (Δ BFE) = 2 ar (ΔEFD)
Solution
Given that ,
ABC and BDE are two equilateral triangles.
Let AB = BC = CA = x . Then `BD = x/2 = DE = BE`
(1) We have
`ar (ΔABC) =sqrt3/4 x^2`
`ar (ΔABC) =sqrt3/4 (x/2)^2 = 1/4 xx sqrt3/4 x^2 `
⇒ `ar (ΔBDE) =sqrt3/4 (x/2)^2`
(2) It is given that triangles ABC and BED are equilateral triangles
∠ACB =∠DBE = 60°
⇒ BF ll AC (Since alternative angles are equal)
Triangles BAF and BEC are on the same base
BE and between the same parallel BE and AC
∴ ar (ΔBAE) = area (ΔBEC)
⇒ ar (ΔBAE) = area (ΔBDE)
[ ∴ ED is a median of ΔEBC ; ar (ΔBEC) = 2ar (ΔBDE) ]
⇒ area (Δ BDE) =`1/2` ar (Δ BDE)
(3) Since ΔABC and ΔBDE are equilateral triangles
∴ ∠ABC = 60° and ∠BDE = 60°
∠ ABC = ∠BDE
⇒ AB ll DE (Since alternative angles are equal)
Triangles BED and AED are on the same base ED and between the same parallels
AB and DE.
∴ ar (ΔBED) = area (ΔED)
⇒ ar (ΔBED) - area (ΔEFD) = area (AED) - area (ΔEFD)
⇒ ar (BEF) = ar (ΔAFD)
(4) Since ED is the median of ΔBEC
∴ area (ΔBEC) = 2ar (ΔBDE)
⇒ `ar (ΔBEC) = 2 xx 1/4 ar (ΔABC)` [form (1)]
⇒ ar(ΔBEC = area (ΔABC)
⇒ area (ΔABC) = 2area (ΔBEC)
(5) Let h be the height of vertex E, corresponding to the side BD on triangle BDE
Let H be the height of the vertex A corresponding to the side BC in triangle ABC
From part (i)
ar (Δ BDE) = `1/4` ar (ΔABC)
⇒ `1/2 xx BD xx h = 1/4 ar ( Δ ABC)`
⇒ `BD xx h = 1/4 (1/2 xx BC xx H)`
⇒ `h = 1/2 H` ............... (1)
From part …..(3)
Area (ΔBFE) = ar (ΔAFD)
= `1/2 xx FD xx H`
= `1/2 xx FD xxH`
= `2(1/2 xx FD xx 2h)`
= 2ar (Δ EFD)
(6) area (ΔAFC) area ( AFD) + area ( ADC)
⇒ ar (ΔBFE) ar + `1/2` ar (ΔABC)
[ using part (3); and AD is the median ΔABC ]
= ar (ΔBFE +`1/2 xx` 4ar (ΔBDE) using part (1)]
= ar (ΔBFE) =2ar (ΔFED) ....... (3)
Area ( ΔBDE) = ar (ΔBFE) + ar (ΔFED)
⇒ R ar (ΔFED) + ar (Δ FED)
⇒ 3 ar (ΔFED)
From (2), (3) and (4) we get
Area (ΔAFC) = 2area (ΔFED) + 2 × 3ar (ΔFED)
= 8 ar (ΔFED)
Hence, area `(ΔFED) = 1/8`area (AFC)
APPEARS IN
RELATED QUESTIONS
In a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = 1/4ar (ABC).
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 1/4ar (ABC)
(iii) ar (BDEF) = 1/2ar (ABC)
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
(i) ar(PRQ) = 1/2 ar(ARC)
(ii) ar(RQC) = 3/8 ar(ABC)
(iii) ar(PBQ) = ar(ARC)
In a ΔABC, if L and M are points on AB and AC respectively such that LM || BC. Prove
that:
(1) ar (ΔLCM ) = ar (ΔLBM )
(2) ar (ΔLBC) = ar (ΔMBC)
(3) ar (ΔABM) ar (ΔACL)
(4) ar (ΔLOB) ar (ΔMOC)
If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is ______.
ABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = 24 cm2, then ar (ABC) = 24 cm2.
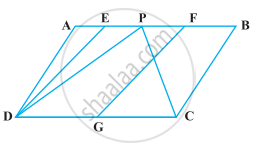
In the following figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then ar (DPC) = `1/2` ar (EFGD).
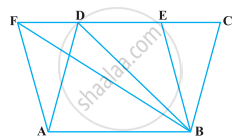
The area of the parallelogram ABCD is 90 cm2 (see figure). Find
- ar (ΔABEF)
- ar (ΔABD)
- ar (ΔBEF)
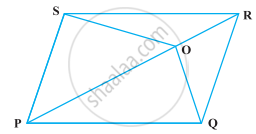
O is any point on the diagonal PR of a parallelogram PQRS (Figure). Prove that ar (PSO) = ar (PQO).