Advertisements
Advertisements
Question
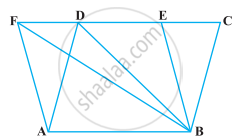
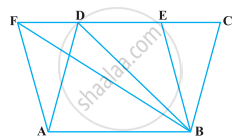
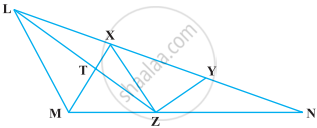
The area of the parallelogram ABCD is 90 cm2 (see figure). Find
- ar (ΔABEF)
- ar (ΔABD)
- ar (ΔBEF)
Solution
Given, area of parallelogram, ABCD = 90 cm2.
i. We know that, parallelograms on the same base and between the same parallel are equal in areas.
Here, parallelograms ABCD and ABEF are on same base AB and between the same parallels AB and CF.
So, ar (ΔBEF) = ar (ABCD) = 90 cm2
ii. We know that, if a triangle and a parallelogram are on the same base and between the same parallels, then area of triangle is equal to half of the area of the parallelogram.
Here, ΔABD and parallelogram ABCD are on the same base AB and between the same parallels AB and CD.
So, ar (ΔABD) = `1/2` ar (ABCD)
= `1/2 xx 90` ...[∴ ar (ABCD) = 90 cm2]
= 45 cm2
iii. Here, ABEF and parallelogram ABEF are on the same base EF and between the same parallels AB and EF.
ar (ΔBEF) = `1/2` ar (ABEF)
= `1/2 xx 90` ...[∴ ar (ABEF) = 90 cm2, from part (i)]
= 45 cm2
APPEARS IN
RELATED QUESTIONS
XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that
ar (ABE) = ar (ACF)
Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
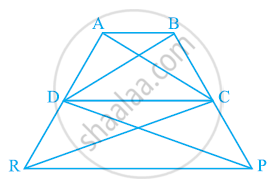
In the given figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
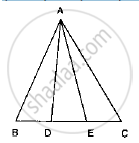
In the below fig. D and E are two points on BC such that BD = DE = EC. Show that ar
(ΔABD) = ar (ΔADE) = ar (ΔAEC).
If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is ______.
ABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = 24 cm2, then ar (ABC) = 24 cm2.
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE) = `1/4` ar (ABC).
In the following figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then ar (DPC) = `1/2` ar (EFGD).
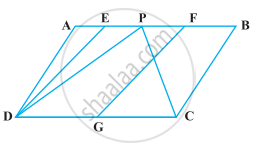
X and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z (See figure). Prove that ar (LZY) = ar (MZYX)
The area of the parallelogram ABCD is 90 cm2 (see figure). Find ar (ΔABD)