Advertisements
Advertisements
Question
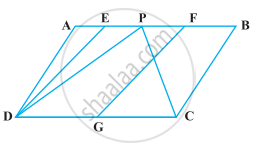
In the following figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then ar (DPC) = `1/2` ar (EFGD).
Options
True
False
Solution
This statement is False.
Explanation:
In the given figure, join PG.
Since, G is the mid-point of CD.
Thus, PG is a median of ΔDPC and it divides the triangle into parts of equal areas.
Then, ar (ΔDPG) = ar (ΔGPC) = `1/2` ar (ΔDPC) ...(i)
Also, we know that, if a parallelogram and a triangle lie on the same base and between the same parallels, then area of triangle is equal to half of the area of parallelogram.
Here, parallelogram EFGD and ΔDPG lie on the same base DG and between the same parallels DG and EF.
So, ar (ΔDPG) = `1/2` ar (EFGD) ...(ii)
From equations (i) and (ii),
`1/2` ar (ΔDPG) = `1/2` ar (EFGD)
⇒ ar (ΔDPC) = ar (EFGD)
APPEARS IN
RELATED QUESTIONS
In the given figure, ABC and ABD are two triangles on the same base AB. If line-segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).
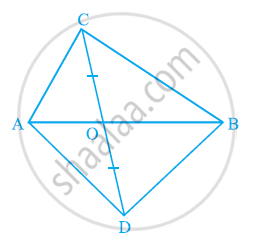
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
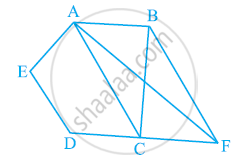
In the given figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
In the given figure, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
In the following figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:-
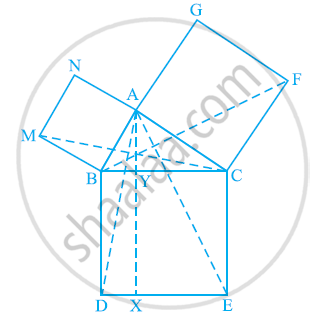
(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar(MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar (CYXE) = ar(ACFG)
(vii) ar (BCED) = ar(ABMN) + ar(ACFG)
Note : Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.
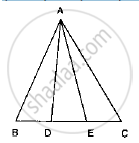
In the below fig. D and E are two points on BC such that BD = DE = EC. Show that ar
(ΔABD) = ar (ΔADE) = ar (ΔAEC).
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE) = `1/4` ar (ABC).
The area of the parallelogram ABCD is 90 cm2 (see figure). Find ar (ΔBEF)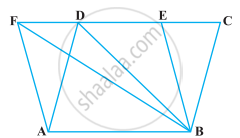
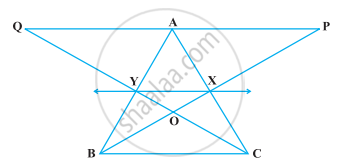
In the following figure, X and Y are the mid-points of AC and AB respectively, QP || BC and CYQ and BXP are straight lines. Prove that ar (ABP) = ar (ACQ).