Advertisements
Advertisements
प्रश्न
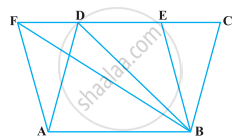
The area of the parallelogram ABCD is 90 cm2 (see figure). Find
- ar (ΔABEF)
- ar (ΔABD)
- ar (ΔBEF)
उत्तर
Given, area of parallelogram, ABCD = 90 cm2.
i. We know that, parallelograms on the same base and between the same parallel are equal in areas.
Here, parallelograms ABCD and ABEF are on same base AB and between the same parallels AB and CF.
So, ar (ΔBEF) = ar (ABCD) = 90 cm2
ii. We know that, if a triangle and a parallelogram are on the same base and between the same parallels, then area of triangle is equal to half of the area of the parallelogram.
Here, ΔABD and parallelogram ABCD are on the same base AB and between the same parallels AB and CD.
So, ar (ΔABD) = `1/2` ar (ABCD)
= `1/2 xx 90` ...[∴ ar (ABCD) = 90 cm2]
= 45 cm2
iii. Here, ABEF and parallelogram ABEF are on the same base EF and between the same parallels AB and EF.
ar (ΔBEF) = `1/2` ar (ABEF)
= `1/2 xx 90` ...[∴ ar (ABEF) = 90 cm2, from part (i)]
= 45 cm2
APPEARS IN
संबंधित प्रश्न
D and E are points on sides AB and AC respectively of ΔABC such that
ar (DBC) = ar (EBC). Prove that DE || BC.
In the given figure, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

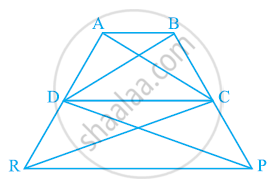
In the given figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
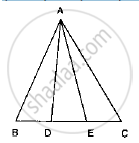
In the below fig. D and E are two points on BC such that BD = DE = EC. Show that ar
(ΔABD) = ar (ΔADE) = ar (ΔAEC).
The area of the parallelogram ABCD is 90 cm2 (see figure). Find ar (ΔABD)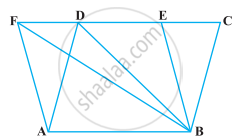
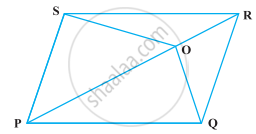
O is any point on the diagonal PR of a parallelogram PQRS (Figure). Prove that ar (PSO) = ar (PQO).
The medians BE and CF of a triangle ABC intersect at G. Prove that the area of ∆GBC = area of the quadrilateral AFGE.
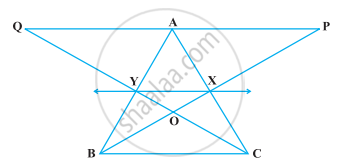
In the following figure, CD || AE and CY || BA. Prove that ar (CBX) = ar (AXY).

In ∆ABC, if L and M are the points on AB and AC, respectively such that LM || BC. Prove that ar (LOB) = ar (MOC)
In the following figure, X and Y are the mid-points of AC and AB respectively, QP || BC and CYQ and BXP are straight lines. Prove that ar (ABP) = ar (ACQ).