Advertisements
Advertisements
प्रश्न
In ∆ABC, if L and M are the points on AB and AC, respectively such that LM || BC. Prove that ar (LOB) = ar (MOC)
उत्तर
Given: In ΔABC, L and M are points on AB and AC respectively such that LM || BC.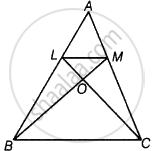
To prove: ar (ΔLOB) = ar (ΔMOC)
Proof: We know that, triangles on the same base and between the same base between the same parallels are equal in area.
Hence, ΔLBC and ΔMBC lie on the same base BC and between the same parallels BC and LM.
So, ar (ΔLBC) = ar (ΔMBC)
⇒ ar (ΔLOB) + ar (ΔBOC) = ar (ΔMOC) + ar (ΔBOC)
On eliminating D ar (ΔBOC) from both sides, we get
ar (ΔLOB) = ar (ΔMOC)
Hence proved.
APPEARS IN
संबंधित प्रश्न
Show that the diagonals of a parallelogram divide it into four triangles of equal area.
D and E are points on sides AB and AC respectively of ΔABC such that
ar (DBC) = ar (EBC). Prove that DE || BC.
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see the following figure). Show that
ar (ABCD) = ar (PBQR).
[Hint: Join AC and PQ. Now compare area (ACQ) and area (APQ)]
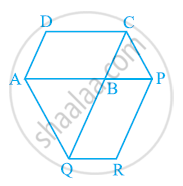
Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
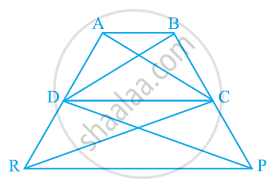
In the given figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
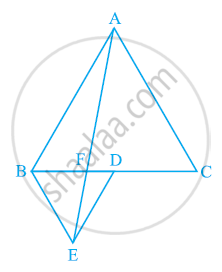
(i) ar (BDE) = 1/4 ar (ABC)
(ii) ar (BDE) = 1/2 ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 1/8 ar (AFC)
[Hint : Join EC and AD. Show that BE || AC and DE || AB, etc.]
In the following figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:-
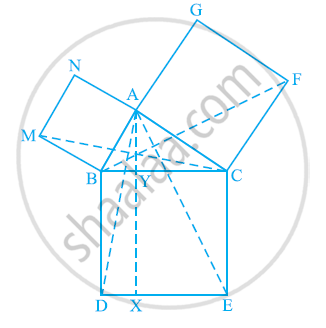
(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar(MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar (CYXE) = ar(ACFG)
(vii) ar (BCED) = ar(ABMN) + ar(ACFG)
Note : Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.
In Fig. below, ABC and BDE are two equilateral triangles such that D is the mid-point of
BC. AE intersects BC in F. Prove that
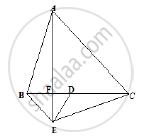
(1) ar (Δ BDE) = `1/2` ar (ΔABC)
(2) Area ( ΔBDE) `= 1/2 ` ar (ΔBAE)
(3) ar (BEF) = ar (ΔAFD)
(4) area (Δ ABC) = 2 area (ΔBEC)
(5) ar (ΔFED) `= 1/8` ar (ΔAFC)
(6) ar (Δ BFE) = 2 ar (ΔEFD)
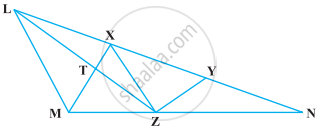
X and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z (See figure). Prove that ar (LZY) = ar (MZYX)
The area of the parallelogram ABCD is 90 cm2 (see figure). Find ar (ΔBEF)