Advertisements
Advertisements
प्रश्न
In Fig. below, ABC and BDE are two equilateral triangles such that D is the mid-point of
BC. AE intersects BC in F. Prove that
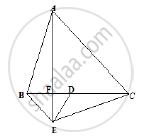
(1) ar (Δ BDE) = `1/2` ar (ΔABC)
(2) Area ( ΔBDE) `= 1/2 ` ar (ΔBAE)
(3) ar (BEF) = ar (ΔAFD)
(4) area (Δ ABC) = 2 area (ΔBEC)
(5) ar (ΔFED) `= 1/8` ar (ΔAFC)
(6) ar (Δ BFE) = 2 ar (ΔEFD)
उत्तर
Given that ,
ABC and BDE are two equilateral triangles.
Let AB = BC = CA = x . Then `BD = x/2 = DE = BE`
(1) We have
`ar (ΔABC) =sqrt3/4 x^2`
`ar (ΔABC) =sqrt3/4 (x/2)^2 = 1/4 xx sqrt3/4 x^2 `
⇒ `ar (ΔBDE) =sqrt3/4 (x/2)^2`
(2) It is given that triangles ABC and BED are equilateral triangles
∠ACB =∠DBE = 60°
⇒ BF ll AC (Since alternative angles are equal)
Triangles BAF and BEC are on the same base
BE and between the same parallel BE and AC
∴ ar (ΔBAE) = area (ΔBEC)
⇒ ar (ΔBAE) = area (ΔBDE)
[ ∴ ED is a median of ΔEBC ; ar (ΔBEC) = 2ar (ΔBDE) ]
⇒ area (Δ BDE) =`1/2` ar (Δ BDE)
(3) Since ΔABC and ΔBDE are equilateral triangles
∴ ∠ABC = 60° and ∠BDE = 60°
∠ ABC = ∠BDE
⇒ AB ll DE (Since alternative angles are equal)
Triangles BED and AED are on the same base ED and between the same parallels
AB and DE.
∴ ar (ΔBED) = area (ΔED)
⇒ ar (ΔBED) - area (ΔEFD) = area (AED) - area (ΔEFD)
⇒ ar (BEF) = ar (ΔAFD)
(4) Since ED is the median of ΔBEC
∴ area (ΔBEC) = 2ar (ΔBDE)
⇒ `ar (ΔBEC) = 2 xx 1/4 ar (ΔABC)` [form (1)]
⇒ ar(ΔBEC = area (ΔABC)
⇒ area (ΔABC) = 2area (ΔBEC)
(5) Let h be the height of vertex E, corresponding to the side BD on triangle BDE
Let H be the height of the vertex A corresponding to the side BC in triangle ABC
From part (i)
ar (Δ BDE) = `1/4` ar (ΔABC)
⇒ `1/2 xx BD xx h = 1/4 ar ( Δ ABC)`
⇒ `BD xx h = 1/4 (1/2 xx BC xx H)`
⇒ `h = 1/2 H` ............... (1)
From part …..(3)
Area (ΔBFE) = ar (ΔAFD)
= `1/2 xx FD xx H`
= `1/2 xx FD xxH`
= `2(1/2 xx FD xx 2h)`
= 2ar (Δ EFD)
(6) area (ΔAFC) area ( AFD) + area ( ADC)
⇒ ar (ΔBFE) ar + `1/2` ar (ΔABC)
[ using part (3); and AD is the median ΔABC ]
= ar (ΔBFE +`1/2 xx` 4ar (ΔBDE) using part (1)]
= ar (ΔBFE) =2ar (ΔFED) ....... (3)
Area ( ΔBDE) = ar (ΔBFE) + ar (ΔFED)
⇒ R ar (ΔFED) + ar (Δ FED)
⇒ 3 ar (ΔFED)
From (2), (3) and (4) we get
Area (ΔAFC) = 2area (ΔFED) + 2 × 3ar (ΔFED)
= 8 ar (ΔFED)
Hence, area `(ΔFED) = 1/8`area (AFC)
APPEARS IN
संबंधित प्रश्न
Show that the diagonals of a parallelogram divide it into four triangles of equal area.
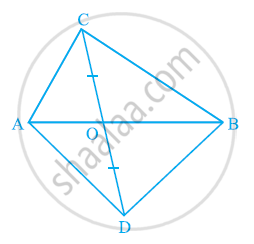
In the given figure, ABC and ABD are two triangles on the same base AB. If line-segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 1/4ar (ABC)
(iii) ar (BDEF) = 1/2ar (ABC)
D and E are points on sides AB and AC respectively of ΔABC such that
ar (DBC) = ar (EBC). Prove that DE || BC.
In the following figure, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you answer the question that you have left in the ’Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
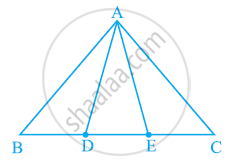
[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ΔABC into n triangles of equal areas.]
In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
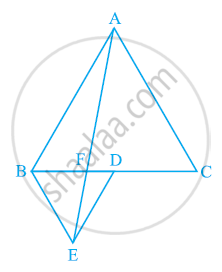
(i) ar (BDE) = 1/4 ar (ABC)
(ii) ar (BDE) = 1/2 ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 1/8 ar (AFC)
[Hint : Join EC and AD. Show that BE || AC and DE || AB, etc.]
PQRS is a parallelogram whose area is 180 cm2 and A is any point on the diagonal QS. The area of ∆ASR = 90 cm2.
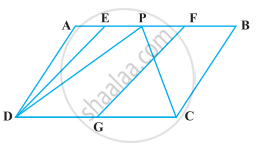
In the following figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then ar (DPC) = `1/2` ar (EFGD).
The area of the parallelogram ABCD is 90 cm2 (see figure). Find ar (ΔABD)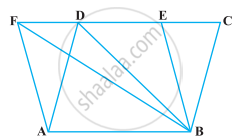
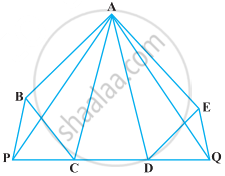
In the following figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (APQ)