Advertisements
Advertisements
प्रश्न
Show that the diagonals of a parallelogram divide it into four triangles of equal area.
उत्तर
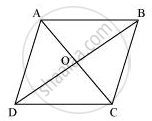
We know that diagonals of parallelogram bisect each other.
Therefore, O is the mid-point of AC and BD.
BO is the median in ΔABC. Therefore, it will divide it into two triangles of equal areas.
∴ Area (ΔAOB) = Area (ΔBOC) ... (1)
In ΔBCD, CO is the median.
∴ Area (ΔBOC) = Area (ΔCOD) ... (2)
Similarly, Area (ΔCOD) = Area (ΔAOD) ... (3)
From equations (1), (2), and (3), we obtain
Area (ΔAOB) = Area (ΔBOC) = Area (ΔCOD) = Area (ΔAOD)
Therefore, it is evident that the diagonals of a parallelogram divide it into four triangles of equal area.
APPEARS IN
संबंधित प्रश्न
Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPC).
[Hint : From A and C, draw perpendiculars to BD.]
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
(i) ar(PRQ) = 1/2 ar(ARC)
(ii) ar(RQC) = 3/8 ar(ABC)
(iii) ar(PBQ) = ar(ARC)
In a ΔABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point
of AP. Prove that :
(1) ar (Δ PBQ) = ar (Δ ARC)
(2) ar (Δ PRQ) =`1/2`ar (Δ ARC)
(3) ar (Δ RQC) =`3/8` ar (Δ ABC) .
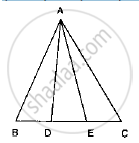
In the below fig. D and E are two points on BC such that BD = DE = EC. Show that ar
(ΔABD) = ar (ΔADE) = ar (ΔAEC).
If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is ______.
ABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = 24 cm2, then ar (ABC) = 24 cm2.
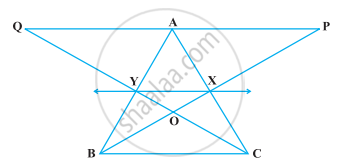
In the following figure, CD || AE and CY || BA. Prove that ar (CBX) = ar (AXY).

If the medians of a ∆ABC intersect at G, show that ar (AGB) = ar (AGC) = ar (BGC) = `1/3` ar (ABC)
In the following figure, X and Y are the mid-points of AC and AB respectively, QP || BC and CYQ and BXP are straight lines. Prove that ar (ABP) = ar (ACQ).