Advertisements
Advertisements
प्रश्न
Show that the diagonals of a parallelogram divide it into four triangles of equal area.
उत्तर
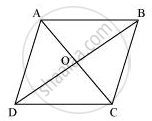
We know that diagonals of parallelogram bisect each other.
Therefore, O is the mid-point of AC and BD.
BO is the median in ΔABC. Therefore, it will divide it into two triangles of equal areas.
∴ Area (ΔAOB) = Area (ΔBOC) ... (1)
In ΔBCD, CO is the median.
∴ Area (ΔBOC) = Area (ΔCOD) ... (2)
Similarly, Area (ΔCOD) = Area (ΔAOD) ... (3)
From equations (1), (2), and (3), we obtain
Area (ΔAOB) = Area (ΔBOC) = Area (ΔCOD) = Area (ΔAOD)
Therefore, it is evident that the diagonals of a parallelogram divide it into four triangles of equal area.
APPEARS IN
संबंधित प्रश्न
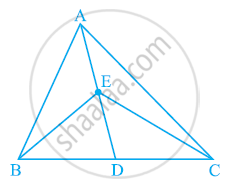
In the given figure, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE)
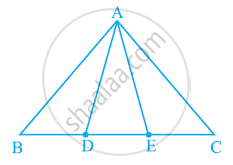
In the following figure, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you answer the question that you have left in the ’Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
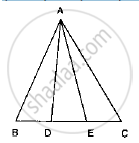
[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ΔABC into n triangles of equal areas.]
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPC).
[Hint : From A and C, draw perpendiculars to BD.]
In the below fig. D and E are two points on BC such that BD = DE = EC. Show that ar
(ΔABD) = ar (ΔADE) = ar (ΔAEC).
If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is ______.
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE) = `1/4` ar (ABC).
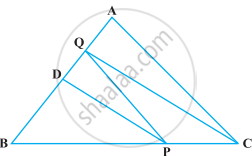
In ∆ABC, D is the mid-point of AB and P is any point on BC. If CQ || PD meets AB in Q (Figure), then prove that ar (BPQ) = `1/2` ar (∆ABC).
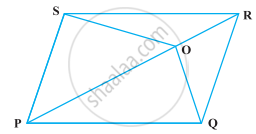
O is any point on the diagonal PR of a parallelogram PQRS (Figure). Prove that ar (PSO) = ar (PQO).
A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar (ADF) = ar (ABFC)
The medians BE and CF of a triangle ABC intersect at G. Prove that the area of ∆GBC = area of the quadrilateral AFGE.
