Advertisements
Advertisements
प्रश्न
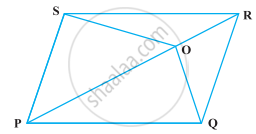
O is any point on the diagonal PR of a parallelogram PQRS (Figure). Prove that ar (PSO) = ar (PQO).
उत्तर
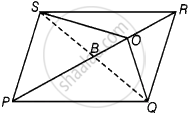
Given: In a parallelogram PQRS, O is any point on the diagonal PR.
To prove: ar (ΔPSO) = ar (ΔPQO)
Construction: Join SQ which intersect PR at B.
Proof: We know that, diagonals of a parallelogram bisect each other, so B is the mid-point of SQ.
Here, PB is a median of ΔQPS and we know that, a median of a triangle divides it into two triangles of equal area.
∴ ar (ΔBPQ) = ar (ΔBPS) ...(i)
Also, OB is the median of ΔOSQ.
∴ ar (ΔOBQ) = ar (ΔOBS) ...(ii)
On adding equations (i) and (ii), we get
ar (ΔBPQ) + ar (ΔOBQ) = ar (ΔBPS) + ar (ΔOBS)
⇒ ar (ΔPQO) = ar (ΔPSO)
Hence proved.
APPEARS IN
संबंधित प्रश्न
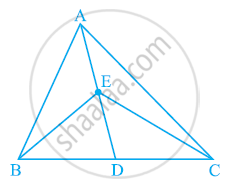
In the given figure, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE)
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 1/4ar (ABC)
(iii) ar (BDEF) = 1/2ar (ABC)
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
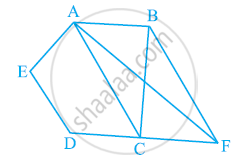
In the given figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
In the following figure, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you answer the question that you have left in the ’Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
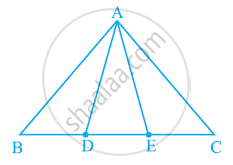
[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ΔABC into n triangles of equal areas.]
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPC).
[Hint : From A and C, draw perpendiculars to BD.]
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
(i) ar(PRQ) = 1/2 ar(ARC)
(ii) ar(RQC) = 3/8 ar(ABC)
(iii) ar(PBQ) = ar(ARC)
X and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z (See figure). Prove that ar (LZY) = ar (MZYX)
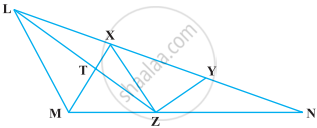
In the following figure, CD || AE and CY || BA. Prove that ar (CBX) = ar (AXY).

In the following figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (APQ)