Advertisements
Advertisements
प्रश्न
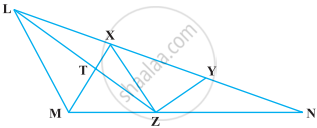
X and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z (See figure). Prove that ar (LZY) = ar (MZYX)
उत्तर
Given: X and Y are points on the side LN such that LX = XY = YN and XZ || LM
To prove: ar (ΔLZY) = ar (MZYX)
Proof: Since, ΔXMZ and ΔXLZ are on the same base XZ and between the same parallel lines LM and XZ.
Then, ar (ΔXMZ) = ar (ΔXLZ) ...(i)
On adding ar (ΔXYZ) both sides of equation (i), we get
ar (ΔXMZ) + ar (ΔXXZ) = ar (ΔXLZ) + ar (ΔXYZ)
⇒ ar (MZYX) = ar (ΔLZY)
Hence proved.
APPEARS IN
संबंधित प्रश्न
Show that the diagonals of a parallelogram divide it into four triangles of equal area.
XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that
ar (ABE) = ar (ACF)
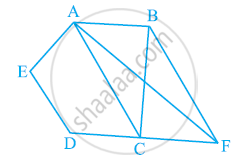
In the given figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY).
[Hint: Join CX.]
In the given figure, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

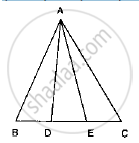
In the following figure, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you answer the question that you have left in the ’Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
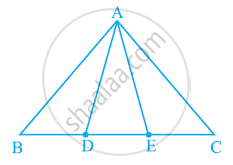
[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ΔABC into n triangles of equal areas.]
In the below fig. D and E are two points on BC such that BD = DE = EC. Show that ar
(ΔABD) = ar (ΔADE) = ar (ΔAEC).
In a ΔABC, if L and M are points on AB and AC respectively such that LM || BC. Prove
that:
(1) ar (ΔLCM ) = ar (ΔLBM )
(2) ar (ΔLBC) = ar (ΔMBC)
(3) ar (ΔABM) ar (ΔACL)
(4) ar (ΔLOB) ar (ΔMOC)
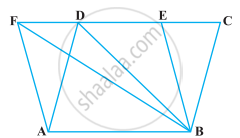
The area of the parallelogram ABCD is 90 cm2 (see figure). Find
- ar (ΔABEF)
- ar (ΔABD)
- ar (ΔBEF)
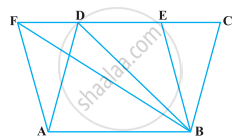
The area of the parallelogram ABCD is 90 cm2 (see figure). Find ar (ΔBEF)