Advertisements
Advertisements
प्रश्न
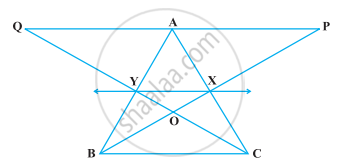
XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that
ar (ABE) = ar (ACF)
उत्तर
It is given that
XY || BC ⇒ EY || BC
BE || AC ⇒ BE || CY
Therefore, EBCY is a parallelogram.
It is given that
XY || BC ⇒ XF || BC
FC || AB ⇒ FC || XB
Therefore, BCFX is a parallelogram.
Parallelograms EBCY and BCFX are on the same base BC and between the same parallels BC and EF.
∴ Area (EBCY) = Area (BCFX) ... (1)
Consider parallelogram EBCY and ΔAEB
These lie on the same base BE and are between the same parallels BE and AC.
∴ Area (ΔABE) = 1/2Area (EBCY) ... (2)
Also, parallelogram BCFX and ΔACF are on the same base CF and between the same parallels CF and AB.
∴ Area (ΔACF) = 1/2Area (BCFX) ... (3)
From equations (1), (2), and (3), we obtain
Area (ΔABE) = Area (ΔACF)
APPEARS IN
संबंधित प्रश्न
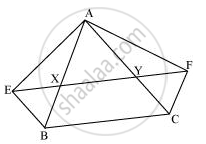
In the given figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
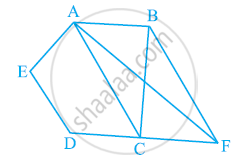
In the given figure, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

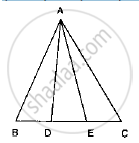
In the below fig. D and E are two points on BC such that BD = DE = EC. Show that ar
(ΔABD) = ar (ΔADE) = ar (ΔAEC).
If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is ______.
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE) = `1/4` ar (ABC).
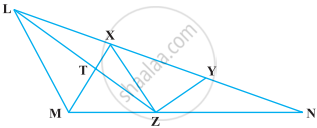
X and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z (See figure). Prove that ar (LZY) = ar (MZYX)
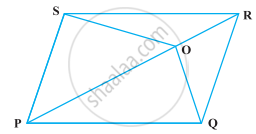
O is any point on the diagonal PR of a parallelogram PQRS (Figure). Prove that ar (PSO) = ar (PQO).
A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar (ADF) = ar (ABFC)
In the following figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (APQ)
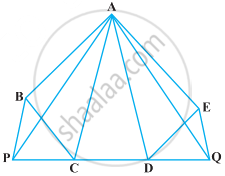
In the following figure, X and Y are the mid-points of AC and AB respectively, QP || BC and CYQ and BXP are straight lines. Prove that ar (ABP) = ar (ACQ).