Advertisements
Advertisements
प्रश्न
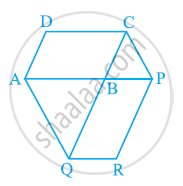
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see the following figure). Show that
ar (ABCD) = ar (PBQR).
[Hint: Join AC and PQ. Now compare area (ACQ) and area (APQ)]
उत्तर
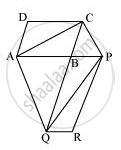
Let us join AC and PQ.
ΔACQ and ΔAQP are on the same base AQ and between the same parallels AQ and CP.
∴ Area (ΔACQ) = Area (ΔAPQ)
⇒ Area (ΔACQ) − Area (ΔABQ) = Area (ΔAPQ) − Area (ΔABQ)
⇒ Area (ΔABC) = Area (ΔQBP) ... (1)
Since AC and PQ are diagonals of parallelograms ABCD and PBQR respectively,
∴ Area (ΔABC) = 1/2Area (ABCD) ... (2)
Area (ΔQBP) = 1/2Area (PBQR) ... (3)
From equations (1), (2), and (3), we obtain
1/2Area (ABCD) = 1/2Area (PBQR)
Area (ABCD) = Area (PBQR)
APPEARS IN
संबंधित प्रश्न
D and E are points on sides AB and AC respectively of ΔABC such that
ar (DBC) = ar (EBC). Prove that DE || BC.
XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that
ar (ABE) = ar (ACF)
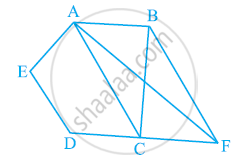
In the given figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
(i) ar(PRQ) = 1/2 ar(ARC)
(ii) ar(RQC) = 3/8 ar(ABC)
(iii) ar(PBQ) = ar(ARC)
ABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = 24 cm2, then ar (ABC) = 24 cm2.
The area of the parallelogram ABCD is 90 cm2 (see figure). Find ar (ΔBEF)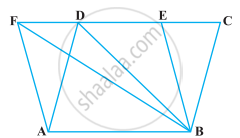
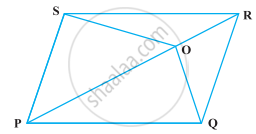
O is any point on the diagonal PR of a parallelogram PQRS (Figure). Prove that ar (PSO) = ar (PQO).
A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar (ADF) = ar (ABFC)
In the following figure, CD || AE and CY || BA. Prove that ar (CBX) = ar (AXY).

In ∆ABC, if L and M are the points on AB and AC, respectively such that LM || BC. Prove that ar (LOB) = ar (MOC)
