Advertisements
Advertisements
प्रश्न
In the following figure, CD || AE and CY || BA. Prove that ar (CBX) = ar (AXY).

उत्तर
Given: In the following figure, CD || AE and CY || BA
To prove: ar (ΔCBX) = ar (ΔAXY) .
Proof: We know that, triangles on the same base and between the same parallels are equal in areas.
Here, ΔABY and ΔABC both lie on the same base AB and between the same parallels CY and BA.
ar (ΔABY) = ar (ΔABC)
⇒ ar (ABX) + ar (AXY) = ar (ABX) + ar (CBX)
⇒ ar (AXY) = ar (CBX) ...[Eliminating ar (ABX) from both sides]
APPEARS IN
संबंधित प्रश्न
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see the following figure). Show that
ar (ABCD) = ar (PBQR).
[Hint: Join AC and PQ. Now compare area (ACQ) and area (APQ)]
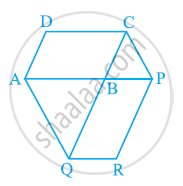
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
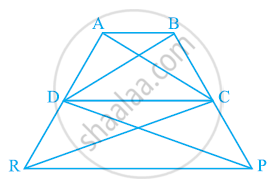
In the given figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
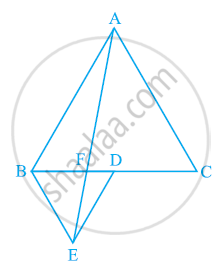
(i) ar (BDE) = 1/4 ar (ABC)
(ii) ar (BDE) = 1/2 ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 1/8 ar (AFC)
[Hint : Join EC and AD. Show that BE || AC and DE || AB, etc.]
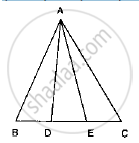
In the below fig. D and E are two points on BC such that BD = DE = EC. Show that ar
(ΔABD) = ar (ΔADE) = ar (ΔAEC).
PQRS is a parallelogram whose area is 180 cm2 and A is any point on the diagonal QS. The area of ∆ASR = 90 cm2.
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE) = `1/4` ar (ABC).
In the following figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then ar (DPC) = `1/2` ar (EFGD).
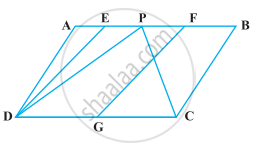
In ∆ABC, D is the mid-point of AB and P is any point on BC. If CQ || PD meets AB in Q (Figure), then prove that ar (BPQ) = `1/2` ar (∆ABC).
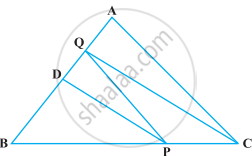
If the medians of a ∆ABC intersect at G, show that ar (AGB) = ar (AGC) = ar (BGC) = `1/3` ar (ABC)
