Advertisements
Advertisements
प्रश्न
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE) = `1/4` ar (ABC).
पर्याय
True
False
उत्तर
This statement is True.
Explanation:
Given: ΔABC and ΔBDE are two equilateral triangles.
Suppose that each sides of triangle ABC be x.
Similarly, D is the mid-point of BC.
So, each side of triangle BDE is `x/2`.
Now, `(Area(ΔBDE))/(Area(ΔABC)) = (sqrt(3)/4 xx (x/2)^2)/(sqrt(3) / 4 xx x^2)`
= `x^2/(4x^2)`
= `1/4`
Therefore, area (ΔBDE) = `1/4` area (ΔABC).
APPEARS IN
संबंधित प्रश्न
In a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = 1/4ar (ABC).
In the given figure, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPC).
[Hint : From A and C, draw perpendiculars to BD.]
In a ΔABC, if L and M are points on AB and AC respectively such that LM || BC. Prove
that:
(1) ar (ΔLCM ) = ar (ΔLBM )
(2) ar (ΔLBC) = ar (ΔMBC)
(3) ar (ΔABM) ar (ΔACL)
(4) ar (ΔLOB) ar (ΔMOC)
PQRS is a parallelogram whose area is 180 cm2 and A is any point on the diagonal QS. The area of ∆ASR = 90 cm2.
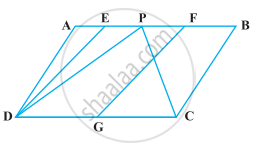
In the following figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then ar (DPC) = `1/2` ar (EFGD).
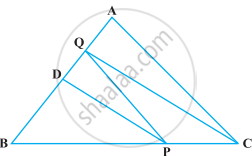
In ∆ABC, D is the mid-point of AB and P is any point on BC. If CQ || PD meets AB in Q (Figure), then prove that ar (BPQ) = `1/2` ar (∆ABC).
The medians BE and CF of a triangle ABC intersect at G. Prove that the area of ∆GBC = area of the quadrilateral AFGE.
In the following figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (APQ)
In the following figure, X and Y are the mid-points of AC and AB respectively, QP || BC and CYQ and BXP are straight lines. Prove that ar (ABP) = ar (ACQ).