Advertisements
Advertisements
प्रश्न
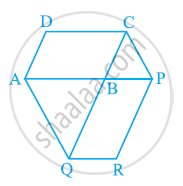
In the given figure, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

उत्तर
Since ΔABQ and ΔPBQ lie on the same base BQ and are between the same parallels AP and BQ,
∴ Area (ΔABQ) = Area (ΔPBQ) ... (1)
Again, ΔBCQ and ΔBRQ lie on the same base BQ and are between the same parallels BQ and CR.
∴ Area (ΔBCQ) = Area (ΔBRQ) ... (2)
On adding equations (1) and (2), we obtain
Area (ΔABQ) + Area (ΔBCQ) = Area (ΔPBQ) + Area (ΔBRQ)
⇒ Area (ΔAQC) = Area (ΔPBR)
APPEARS IN
संबंधित प्रश्न
In a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = 1/4ar (ABC).
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 1/4ar (ABC)
(iii) ar (BDEF) = 1/2ar (ABC)
In the given figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint: From D and B, draw perpendiculars to AC.]

The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see the following figure). Show that
ar (ABCD) = ar (PBQR).
[Hint: Join AC and PQ. Now compare area (ACQ) and area (APQ)]
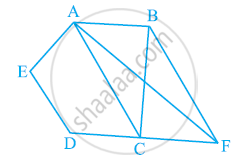
In the given figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
In Fig. below, ABC and BDE are two equilateral triangles such that D is the mid-point of
BC. AE intersects BC in F. Prove that
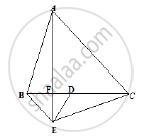
(1) ar (Δ BDE) = `1/2` ar (ΔABC)
(2) Area ( ΔBDE) `= 1/2 ` ar (ΔBAE)
(3) ar (BEF) = ar (ΔAFD)
(4) area (Δ ABC) = 2 area (ΔBEC)
(5) ar (ΔFED) `= 1/8` ar (ΔAFC)
(6) ar (Δ BFE) = 2 ar (ΔEFD)
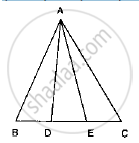
In the below fig. D and E are two points on BC such that BD = DE = EC. Show that ar
(ΔABD) = ar (ΔADE) = ar (ΔAEC).
PQRS is a parallelogram whose area is 180 cm2 and A is any point on the diagonal QS. The area of ∆ASR = 90 cm2.
The area of the parallelogram ABCD is 90 cm2 (see figure). Find ar (ΔBEF)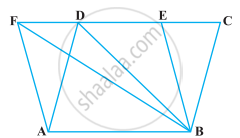
In the following figure, CD || AE and CY || BA. Prove that ar (CBX) = ar (AXY).

