Advertisements
Advertisements
प्रश्न
Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
उत्तर
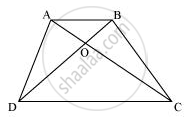
It is given that
Area (ΔAOD) = Area (ΔBOC)
Area (ΔAOD) + Area (ΔAOB) = Area (ΔBOC) + Area (ΔAOB)
Area (ΔADB) = Area (ΔACB)
We know that triangles on the same base having areas equal to each other lie between the same parallels.
Therefore, these triangles, ΔADB and ΔACB, are lying between the same parallels.
i.e., AB || CD
Therefore, ABCD is a trapezium.
APPEARS IN
संबंधित प्रश्न
In the given figure, ABC and ABD are two triangles on the same base AB. If line-segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).
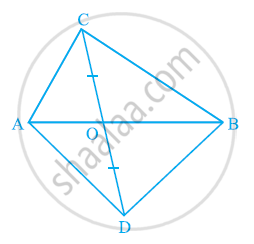
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 1/4ar (ABC)
(iii) ar (BDEF) = 1/2ar (ABC)
D and E are points on sides AB and AC respectively of ΔABC such that
ar (DBC) = ar (EBC). Prove that DE || BC.
In the given figure, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

In Fig. below, ABC and BDE are two equilateral triangles such that D is the mid-point of
BC. AE intersects BC in F. Prove that
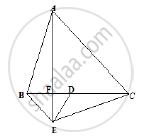
(1) ar (Δ BDE) = `1/2` ar (ΔABC)
(2) Area ( ΔBDE) `= 1/2 ` ar (ΔBAE)
(3) ar (BEF) = ar (ΔAFD)
(4) area (Δ ABC) = 2 area (ΔBEC)
(5) ar (ΔFED) `= 1/8` ar (ΔAFC)
(6) ar (Δ BFE) = 2 ar (ΔEFD)
If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is ______.
A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar (ADF) = ar (ABFC)
In the following figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (APQ)
If the medians of a ∆ABC intersect at G, show that ar (AGB) = ar (AGC) = ar (BGC) = `1/3` ar (ABC)
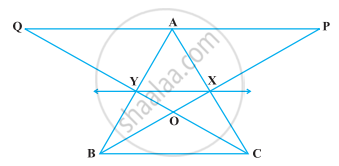
In the following figure, X and Y are the mid-points of AC and AB respectively, QP || BC and CYQ and BXP are straight lines. Prove that ar (ABP) = ar (ACQ).