Advertisements
Advertisements
प्रश्न
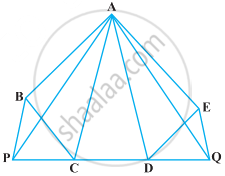
In the following figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (APQ)
उत्तर
Given: ABCDE is a pentagon.
BP || AC and EQ|| AD.
To prove: ar (ABCDE) = ar (APQ)
Proof: We know that, triangles on the same base and between the same parallels are equal in area.
Here, ΔADQ and ΔADE lie on the same base AD and between the same parallels AD and EQ.
So, ar (ΔADQ) = ar (ΔADE) ...(i)
Similarly, ΔACP and ΔACB lie on the same base AC and between the same parallels AC and BP.
So, ar (ΔACP) = ar (ΔACB) ...(ii)
On adding equations (i) and (ii), we get
ar (ΔADQ) + ar (ΔACP) = ar (ΔADE) + ar (ΔACB)
On adding ar (ΔACD) both sides, we get
ar (ΔADQ) + ar (ΔACP) + ar (ΔACD) = ar (ΔADE) + ar (ΔACB) + ar (ΔACD)
⇒ ar (ΔAPQ) = ar (ABCDE)
Hence proved.
APPEARS IN
संबंधित प्रश्न
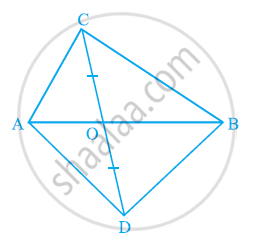
In the given figure, ABC and ABD are two triangles on the same base AB. If line-segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 1/4ar (ABC)
(iii) ar (BDEF) = 1/2ar (ABC)
ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY).
[Hint: Join CX.]
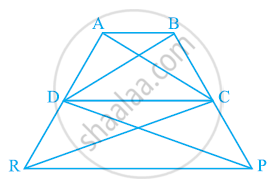
In the given figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPC).
[Hint : From A and C, draw perpendiculars to BD.]
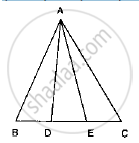
In the below fig. D and E are two points on BC such that BD = DE = EC. Show that ar
(ΔABD) = ar (ΔADE) = ar (ΔAEC).
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE) = `1/4` ar (ABC).
In the following figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then ar (DPC) = `1/2` ar (EFGD).
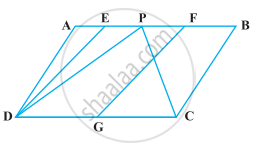
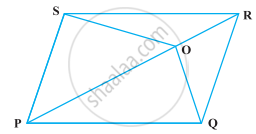
O is any point on the diagonal PR of a parallelogram PQRS (Figure). Prove that ar (PSO) = ar (PQO).
The medians BE and CF of a triangle ABC intersect at G. Prove that the area of ∆GBC = area of the quadrilateral AFGE.
