Advertisements
Advertisements
प्रश्न
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 1/4ar (ABC)
(iii) ar (BDEF) = 1/2ar (ABC)
उत्तर

(i) In ΔABC,
E and F are the mid-points of side AC and AB respectively.
Therefore, EF || BC and EF = 1/2BC (Mid-point theorem)
However, BD = 1/2BC (D is the mid-point of BC)
Therefore, BD = EF and BD || EF
Therefore, BDEF is a parallelogram.
(ii) Using the result obtained above, it can be said that quadrilaterals BDEF, DCEF, AFDE are parallelograms.
We know that diagonal of a parallelogram divides it into two triangles of equal area.
∴Area (ΔBFD) = Area (ΔDEF) (For parallelogram BD)
Area (ΔCDE) = Area (ΔDEF) (For parallelogram DCEF)
Area (ΔAFE) = Area (ΔDEF) (For parallelogram AFDE)
∴Area (ΔAFE) = Area (ΔBFD) = Area (ΔCDE) = Area (ΔDEF)
Also,
Area (ΔAFE) + Area (ΔBDF) + Area (ΔCDE) + Area (ΔDEF) = Area (ΔABC)
⇒ Area (ΔDEF) + Area (ΔDEF) + Area (ΔDEF) + Area (ΔDEF) = Area (ΔABC)
⇒ 4 Area (ΔDEF) = Area (ΔABC)
⇒ Area (ΔDEF) = 1/4Area (ΔABC)
(iii) Area (parallelogram BDEF) = Area (ΔDEF) + Area (ΔBDF)
⇒ Area (parallelogram BDEF) = Area (ΔDEF) + Area (ΔDEF)
⇒ Area (parallelogram BDEF) = 2 Area (ΔDEF)
⇒ Area (parallelogram BDEF)`= 2xx1/4"Area "(ΔABC)`
⇒ Area (parallelogram BDEF) = 1/2Area (ΔABC)
APPEARS IN
संबंधित प्रश्न
In the given figure, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE)
XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that
ar (ABE) = ar (ACF)
In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
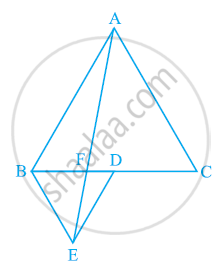
(i) ar (BDE) = 1/4 ar (ABC)
(ii) ar (BDE) = 1/2 ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 1/8 ar (AFC)
[Hint : Join EC and AD. Show that BE || AC and DE || AB, etc.]
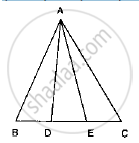
In the below fig. D and E are two points on BC such that BD = DE = EC. Show that ar
(ΔABD) = ar (ΔADE) = ar (ΔAEC).
In a ΔABC, if L and M are points on AB and AC respectively such that LM || BC. Prove
that:
(1) ar (ΔLCM ) = ar (ΔLBM )
(2) ar (ΔLBC) = ar (ΔMBC)
(3) ar (ΔABM) ar (ΔACL)
(4) ar (ΔLOB) ar (ΔMOC)
ABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = 24 cm2, then ar (ABC) = 24 cm2.
PQRS is a parallelogram whose area is 180 cm2 and A is any point on the diagonal QS. The area of ∆ASR = 90 cm2.
A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar (ADF) = ar (ABFC)
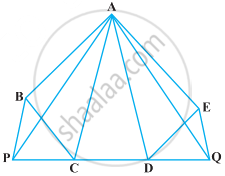
In the following figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (APQ)
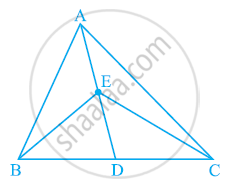
If the medians of a ∆ABC intersect at G, show that ar (AGB) = ar (AGC) = ar (BGC) = `1/3` ar (ABC)
