Advertisements
Advertisements
प्रश्न
In the given figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint: From D and B, draw perpendiculars to AC.]

उत्तर
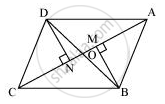
Let us draw DN ⊥ AC and BM ⊥ AC.
(i) In ΔDON and ΔBOM,
∠DNO = ∠BMO (By construction)
∠DON = ∠BOM (Vertically opposite angles)
OD = OB (Given)
By AAS congruence rule,
ΔDON ≅ ΔBOM
∴ DN = BM ... (1)
We know that congruent triangles have equal areas.
∴ Area (ΔDON) = Area (ΔBOM) ... (2)
In ΔDNC and ΔBMA,
∠DNC = ∠BMA (By construction)
CD = AB (Given)
DN = BM [Using equation (1)]
∴ ΔDNC ≅ ΔBMA (RHS congruence rule)
⇒ Area (ΔDNC) = Area (ΔBMA) ... (3)
On adding equations (2) and (3), we obtain
Area (ΔDON) + Area (ΔDNC) = Area (ΔBOM) + Area (ΔBMA)
Therefore, Area (ΔDOC) = Area (ΔAOB)
(ii) We obtained,
Area (ΔDOC) = Area (ΔAOB)
⇒ Area (ΔDOC) + Area (ΔOCB) = Area (ΔAOB) + Area (ΔOCB)
(Adding Area (ΔOCB) to both sides)
⇒ Area (ΔDCB) = Area (ΔACB)
(iii) We obtained,
Area (ΔDCB) = Area (ΔACB)
If two triangles have the same base and equal areas, then these will lie between the same parallels.
∴ DA || CB ... (4)
In ΔDOA and ΔBOC,
∠DOA = ∠BOC (Vertically opposite angles)
OD = OB (Given)
∠ODA = ∠OBC (Alternate opposite angles)
By ASA congruence rule,
ΔDOA ≅ ΔBOC
∴ DA = BC ... (5)
In quadrilateral ABCD, one pair of opposite sides is equal and parallel (AD = BC)
Therefore, ABCD is a parallelogram.
APPEARS IN
संबंधित प्रश्न
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 1/4ar (ABC)
(iii) ar (BDEF) = 1/2ar (ABC)
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see the following figure). Show that
ar (ABCD) = ar (PBQR).
[Hint: Join AC and PQ. Now compare area (ACQ) and area (APQ)]
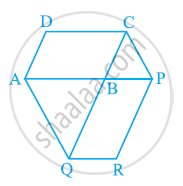
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
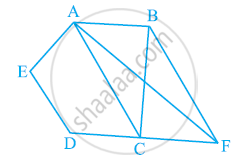
In the given figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
ABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = 24 cm2, then ar (ABC) = 24 cm2.
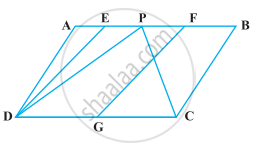
In the following figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then ar (DPC) = `1/2` ar (EFGD).
The area of the parallelogram ABCD is 90 cm2 (see figure). Find ar (ΔBEF)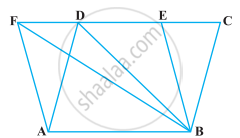
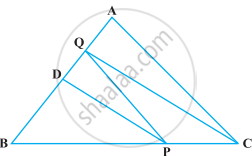
In ∆ABC, D is the mid-point of AB and P is any point on BC. If CQ || PD meets AB in Q (Figure), then prove that ar (BPQ) = `1/2` ar (∆ABC).
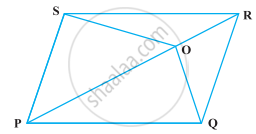
O is any point on the diagonal PR of a parallelogram PQRS (Figure). Prove that ar (PSO) = ar (PQO).
If the medians of a ∆ABC intersect at G, show that ar (AGB) = ar (AGC) = ar (BGC) = `1/3` ar (ABC)
