Advertisements
Advertisements
प्रश्न
D and E are points on sides AB and AC respectively of ΔABC such that
ar (DBC) = ar (EBC). Prove that DE || BC.
उत्तर
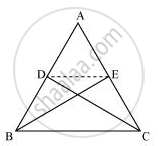
Since ΔBCE and ΔBCD are lying on a common base BC and also have equal areas, ΔBCE and ΔBCD will lie between the same parallel lines.
∴ DE || BC
APPEARS IN
संबंधित प्रश्न
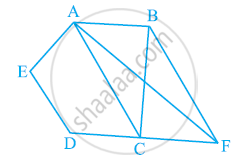
In the given figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
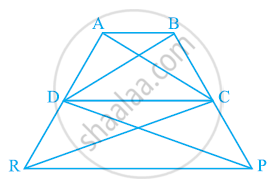
In the given figure, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

In the given figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPC).
[Hint : From A and C, draw perpendiculars to BD.]
In a ΔABC, if L and M are points on AB and AC respectively such that LM || BC. Prove
that:
(1) ar (ΔLCM ) = ar (ΔLBM )
(2) ar (ΔLBC) = ar (ΔMBC)
(3) ar (ΔABM) ar (ΔACL)
(4) ar (ΔLOB) ar (ΔMOC)
The area of the parallelogram ABCD is 90 cm2 (see figure). Find
- ar (ΔABEF)
- ar (ΔABD)
- ar (ΔBEF)
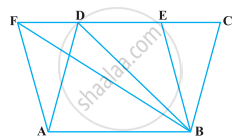
The area of the parallelogram ABCD is 90 cm2 (see figure). Find ar (ΔABD)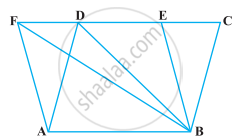
The medians BE and CF of a triangle ABC intersect at G. Prove that the area of ∆GBC = area of the quadrilateral AFGE.
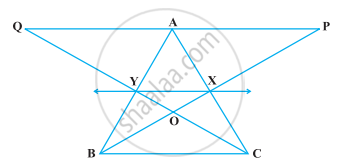
In the following figure, CD || AE and CY || BA. Prove that ar (CBX) = ar (AXY).

In the following figure, X and Y are the mid-points of AC and AB respectively, QP || BC and CYQ and BXP are straight lines. Prove that ar (ABP) = ar (ACQ).