Advertisements
Advertisements
प्रश्न
A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar (ADF) = ar (ABFC)
उत्तर
Given in the question, A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F.
Prove that ar (ADF) = ar (ABFC)
Proof: ABCD is a parallelogram and AC divides it into two triangle of equal area.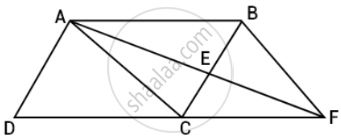
ar (ΔADC) = ar (ΔABC) ...(I)
So, DC || AB and CF || AB
As we know that triangle on the same base and between the same parallels are equal in area.
So, ar (ΔACF) = ar (ΔBCF) ...(II)
Adding equation (I) and (II), we get
ar (ΔADC) + ar (ACF) = ar (ΔABC) + ar (ΔBCF)
ar (ΔADF) = ar (ABFC)
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the given figure, ABC and ABD are two triangles on the same base AB. If line-segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).
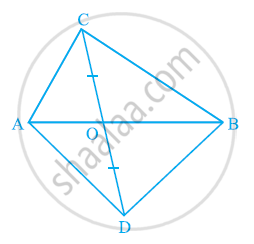
In the given figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint: From D and B, draw perpendiculars to AC.]

XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that
ar (ABE) = ar (ACF)
Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
(i) ar(PRQ) = 1/2 ar(ARC)
(ii) ar(RQC) = 3/8 ar(ABC)
(iii) ar(PBQ) = ar(ARC)
In a ΔABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point
of AP. Prove that :
(1) ar (Δ PBQ) = ar (Δ ARC)
(2) ar (Δ PRQ) =`1/2`ar (Δ ARC)
(3) ar (Δ RQC) =`3/8` ar (Δ ABC) .
In Fig. below, ABC and BDE are two equilateral triangles such that D is the mid-point of
BC. AE intersects BC in F. Prove that
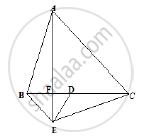
(1) ar (Δ BDE) = `1/2` ar (ΔABC)
(2) Area ( ΔBDE) `= 1/2 ` ar (ΔBAE)
(3) ar (BEF) = ar (ΔAFD)
(4) area (Δ ABC) = 2 area (ΔBEC)
(5) ar (ΔFED) `= 1/8` ar (ΔAFC)
(6) ar (Δ BFE) = 2 ar (ΔEFD)
The area of the parallelogram ABCD is 90 cm2 (see figure). Find ar (ΔABD)
In ∆ABC, D is the mid-point of AB and P is any point on BC. If CQ || PD meets AB in Q (Figure), then prove that ar (BPQ) = `1/2` ar (∆ABC).
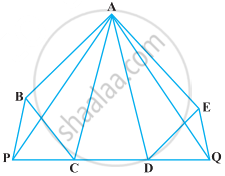
In the following figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (APQ)