Advertisements
Advertisements
प्रश्न
A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar (ADF) = ar (ABFC)
उत्तर
Given in the question, A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F.
Prove that ar (ADF) = ar (ABFC)
Proof: ABCD is a parallelogram and AC divides it into two triangle of equal area.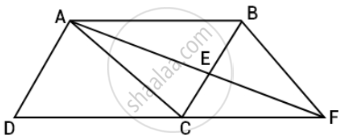
ar (ΔADC) = ar (ΔABC) ...(I)
So, DC || AB and CF || AB
As we know that triangle on the same base and between the same parallels are equal in area.
So, ar (ΔACF) = ar (ΔBCF) ...(II)
Adding equation (I) and (II), we get
ar (ΔADC) + ar (ACF) = ar (ΔABC) + ar (ΔBCF)
ar (ΔADF) = ar (ABFC)
Hence proved.
APPEARS IN
संबंधित प्रश्न
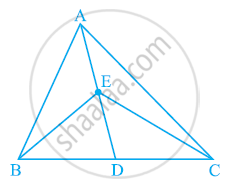
In the given figure, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE)
D and E are points on sides AB and AC respectively of ΔABC such that
ar (DBC) = ar (EBC). Prove that DE || BC.
A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
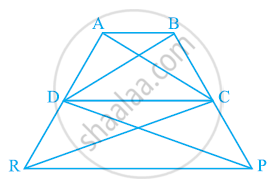
In the given figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
In the following figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:-
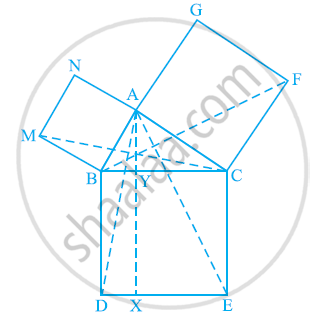
(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar(MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar (CYXE) = ar(ACFG)
(vii) ar (BCED) = ar(ABMN) + ar(ACFG)
Note : Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.
In a ΔABC, if L and M are points on AB and AC respectively such that LM || BC. Prove
that:
(1) ar (ΔLCM ) = ar (ΔLBM )
(2) ar (ΔLBC) = ar (ΔMBC)
(3) ar (ΔABM) ar (ΔACL)
(4) ar (ΔLOB) ar (ΔMOC)
If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is ______.
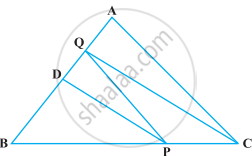
In ∆ABC, D is the mid-point of AB and P is any point on BC. If CQ || PD meets AB in Q (Figure), then prove that ar (BPQ) = `1/2` ar (∆ABC).
In the following figure, CD || AE and CY || BA. Prove that ar (CBX) = ar (AXY).

In the following figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (APQ)